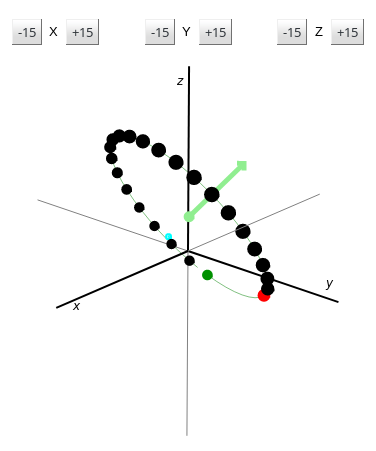
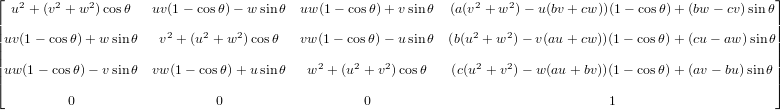A useful method for doing such rotations is to do them with quaternions. In practice, I've found them to be easier to use and have the added bonus of avoiding Gimbal lock.
Here is a nice walk through that explains how and why they are used for rotation about an arbitrary axis (it's the response to the user's question). It's a bit higher level and would be good for someone who is new to the idea, so I recommend starting there.
Update to avoid link corrosion
The text from the linked site:
As you have no doubt already concluded, rotation around the axis
passing through the origin and a point (a,b,c) on the unit sphere in
three-dimensions is a linear transformation, and hence can be
represented by matrix multiplication. We will give a very slick
method for determining this matrix, but to appreciate the compactness
of the formula it will be wise to start with a few remarks.
Rotations in three-dimensions are rather special linear
transformations, not least because they preserve the lengths of
vectors and also (when two vectors are rotated) the angles between the
vectors. Such transformations are called "orthogonal" and they are
represented by orthogonal matrices:
M M' = I
where we conveniently denote the transpose by '. In other words the
transpose of an orthogonal matrix is its inverse.
Consider the data which is needed to define the transformation.
You've already given notation for the axis of rotation, ai + bj + ck,
conveniently assumed to be a unit vector. The only other datum is the
angle of rotation, which for lack of a more natural character I will
denote by r (for rotation?) and which we will assume to be given in
radians.
Now the rotations are actually a bit special even among orthogonal
transformations, and in fact they are also called special orthogonal
transformations (or matrices) in virtue of their property of being
"orientation preserving". Compare them with reflections, which are
also length and angle preserving, and you will find that the geometric
characteristic of preserving orientation (or "handedness" if you
prefer) has a numerical counterpart in the determinant of the matrix.
A rotation's matrix has determinant 1, while a reflection's matrix has
determinant -1. It turns out that the product (or composition) of two
rotations is again a rotation, which agrees with the fact that the
determinant of a product is the product of the determinants (or 1 in
the case of a rotation).
Now we can describe a step by step approach that one might follow to
construct the desired matrix (before we shortcut the whole process and
jump to the Answer!). Consider first a step in which we rotate the
unit vector:
u = ai + bj + ck
so that it coincides with one of the "standard" unit vectors, perhaps
k (the positve z-axis). Now we know how to rotate around the z-axis;
it's a matter of doing the usual 2x2 transformation on the x,y
coordinates alone:
cos(r) sin(r) 0
M = -sin(r) cos(r) 0
0 0 1
Finally we need to "undo" that initial rotation that took u to k,
which is easy because the inverse of that transformation is (we
recall) represented by the matrix transpose. In other words, if
matrix R represents a rotation taking u to k, then R' takes k to u,
and we can write out the composition of transformations like this:
R' M R
It is easily verified that this product of matrices, when multiplied
times u, gives u back again:
R' M R u = R' M k = R' k = u
Therefore this is indeed rotation about the axis defined by u.
One advantage of this expression is that it cleanly separates out the
dependence of M on the angle r from the dependence of Q and Q' on the
"axis" vector u. However if we have to carry out the computations in
detail, we will obviously have a lot of matrix multiplication to do.
So, to the shortcut. It turns out when all the dust settles that the
multiplication among rotations is isomorphic to multiplication of unit
quaternions. Quaternions, in case you've not seen them before, are a
kind of four-dimensional generalization of complex numbers. They were
"invented" by William Hamilton in 1843:
[Sir William Rowan Hamilton]
http://www-gap.dcs.st-and.ac.uk/~history/Mathematicians/Hamilton.html
and today's 3D graphics programmers are greatly in his debt.
Each unit quaternion q = q0 + q1*i + q2*j + q3*k then defines a rotation matrix:
(q0² + q1² - q2² - q3²) 2(q1q2 - q0q3) 2(q1q3 + q0q2)
Q = 2(q2q1 + q0q3) (q0² - q1² + q2² - q3²) 2(q2q3 - q0q1)
2(q3q1 - q0q2) 2(q3q2 + q0q1) (q0² - q1² - q2² + q3²)
To verify that Q is an orthogonal matrix, ie. that Q Q' = I, means in
essence that the rows of Q form an orthonormal basis. So, for
example, the first row should have length 1:
(q0² + q1² - q2² - q3²)² + 4(q1q2 - q0q3)² + 4(q1q3 + q0q2)²
= (q0² + q1² - q2² - q3²)² + 4(q1q2)² + 4(q0q3)² + 4(q1q3)² + 4(q0q2)²
= (q0² + q1² + q2² + q3²)²
= 1
and the first two rows should have dot product zero:
[ (q0² + q1² - q2² - q3²), 2(q1q2 - q0q3), 2(q1q3 + q0q2) ]
* [ 2(q2q1 + q0q3), (q0² - q1² + q2² - q3²), 2(q2q3 - q0q1) ]
= 2(q0² + q1² - q2² - q3²)(q2q1 + q0q3)
+ 2(q1q2 - q0q3)(q0² - q1² + q2² - q3²)
+ 4(q1q3 + q0q2)(q2q3 - q0q1)
= 4(q0²q1q2 + q1²q0q3 - q2²q0q3 - q3²q2q1)
+ 4(q3²q1q2 - q1²q0q3 + q2²q0q3 - q0²q2q1)
= 0
It can also be shown in general that det(Q) = 1, and thus that Q is
really a rotation.
But around what axis is Q the rotation? And by what angle? Well,
given angle r and unit vector:
u = ai + bj + ck
as before, the corresponding quaternion is:
q = cos(r/2) + sin(r/2) * u
= cos(r/2) + sin(r/2) ai + sin(r/2) bj + sin(r/2) ck
Thus with:
q0 = cos(r/2), q1 = sin(r/2) a, q2 = sin(r/2) b, q3 = sin(r/2) c,
we are able to get the desired property that multiplication by Q "fixes" u:
Q u = u
Rather than chug through the long-winded algebra, let's do a simple example.
Let u = 0i + 0.6j + 0.8k be our unit vector and r = pi be our angle of rotation.
Then the quaternion is:
q = cos(pi/2) + sin(pi/2) * u
= 0 + 0i + 0.6j + 0.8k
and the rotation matrix:
-1 0 0
Q = 0 -0.28 0.96
0 0.96 0.28
In this concrete case it is easy to verify that Q Q' = I and det(Q) = 1.
Also we compute that:
Q u = [ 0, -0.28*0.6 + 0.96*0.8, 0.96*0.6 + 0.28*0.8 ]'
= [ 0, 0.6, 0.8 ]'
= u
ie. the unit vector u defines the axis of rotation because it is "fixed" by Q.
Finally we illustrate that the angle of rotation is pi (or 180
degrees) by considering how Q acts on the unit vector in the direction
of the positive x-axis, which is perpendicular to u:
i + 0j + 0k, or as a vector, [ 1, 0, 0 ]'
Then Q [ 1, 0, 0 ]' = [-1, 0, 0 ]' which is the rotation of [ 1, 0, 0
]' through angle pi about u.
As a reference for this representation of rotations by quaternions and
some additional methods of representation (and what they are good
for), see the details here:
[Representing 3D rotations]
http://gandalf-library.sourceforge.net/tutorial/report/node125.html
SUMMARY
Given angle r in radians and unit vector u = ai + bj + ck or [a,b,c]', define:
q0 = cos(r/2), q1 = sin(r/2) a, q2 = sin(r/2) b, q3 = sin(r/2) c
and construct from these values the rotation matrix:
(q0² + q1² - q2² - q3²) 2(q1q2 - q0q3) 2(q1q3 + q0q2)
Q = 2(q2q1 + q0q3) (q0² - q1² + q2² - q3²) 2(q2q3 - q0q1)
2(q3q1 - q0q2) 2(q3q2 + q0q1) (q0² - q1² - q2² + q3²)
Multiplication by Q then effects the desired rotation, and in particular:
Q u = u



![\hat{u} = [u_x,u_y,u_z]](https://static.mcmap.net/file/mcmap/ZG-AbGLDKwfpKnMxcF_AZVLQamyA/HoLjl.png)
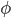
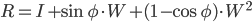
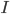
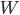
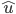
![W= [0 -uz uy; uz 0 -ux; -uy ux 0];](https://static.mcmap.net/file/mcmap/ZG-AbGLDKwfpKnMxcF_AZVLQamyA/V1Fk9.png)