How to know the angle between two vectors?

Question

I am making small game with pygame and I have made a gun that rotates around its center. My problem is that I want the gun to rotate by itself to the enemy direction, but I couldn't do that because I can't find the angle between the gun and the enemy to make the gun rotate to it I have searched and I found that I have to use the atan2 but I didn't find any working code so I hope someone could help me.

Here is my code:

import pygame
from pygame.locals import*
pygame.init()
height=650
width=650
screen=pygame.display.set_mode((height,width))
clock=pygame.time.Clock()
gun=pygame.image.load("m2.png").convert_alpha() 
gun=pygame.transform.smoothscale(gun,(200,200)).convert_alpha()
angle=0
angle_change=0
RED=(255,0,0)
x=525
y=155
while True :
    screen.fill((150,150,150))
    for event in pygame.event.get():
        if event.type==QUIT:
            pygame.quit()
            quit()
        if event.type==KEYDOWN:
            if event.key==K_a:
                angle_change=+1
            if event.key==K_d:
                angle_change=-1
        elif event.type==KEYUP:
            angle_change=0
    angle+=angle_change
    if angle>360:
        angle=0
    if angle<0:
        angle=360
    pygame.draw.rect(screen,RED,(x,y,64,64))
    position = (height/2,width/2)
    gun_rotate=pygame.transform.rotate(gun,angle) 
    rotate_rect = gun_rotate.get_rect()
    rotate_rect.center = position
    screen.blit(gun_rotate, rotate_rect)
    pygame.display.update()
    clock.tick(60) 

And here is a picture trying to make it clear:

How do I solve the problem?

Rhonarhonchus

you may want to plot out the math on paper first prior to implementing it in code. – Undershorts

There is no angle between two points... There is only an angle between three points... – Hazlitt

The angle between two vectors is angle = acos(v1•v2) where • means "dot product"? It sounds like the two vectors here would be defined by the shooter's current location and direction the gun is currently pointing, plus the current location and the location of the enemy. – Rebarebah

@Rebarebah Since the gun and the target are defined relative to implicit x, y axes then tangent = (y2-y1)/(x2-x1) would be used. This allows atan2 to be used. – Linkoski

answer what he meant to ask, not what he asked. In this case I would assume he wants the angle to the next 90 degree split of the coordinate system. – Stinkhorn

Easy: if you have two 2D vectors a and b, then cos(t) = a dot b/mag(a)/mag(b), where mag(x) = sqrt(x1*x1 + x2*x2) – Orangeman

Answer 1

The tangent of the angle between two points is defined as delta y / delta x That is (y2 - y1)/(x2-x1). This means that math.atan2(dy, dx) give the angle between the two points assuming that you know the base axis that defines the co-ordinates.

Your gun is assumed to be the (0, 0) point of the axes in order to calculate the angle in radians. Once you have that angle, then you can use the angle for the remainder of your calculations.

Note that since the angle is in radians, you need to use the math.pi instead of 180 degrees within your code. Also your test for more than 360 degrees (2*math.pi) is not needed. The test for negative (< 0) is incorrect as you then force it to 0, which forces the target to be on the x axis in the positive direction.

Your code to calculate the angle between the gun and the target is thus

myradians = math.atan2(targetY-gunY, targetX-gunX)

If you want to convert radians to degrees

mydegrees = math.degrees(myradians)

To convert from degrees to radians

myradians = math.radians(mydegrees)

Python ATAN2

The Python ATAN2 function is one of the Python Math function which is used to returns the angle (in radians) from the X -Axis to the specified point (y, x).

math.atan2()

Definition Returns the tangent(y,x) in radius.

Syntax
math.atan2(y,x)

Parameters
y,x=numbers

Examples
The return is:

>>> import math  
>>> math.atan2(88,34)  
1.202100424136847  
>>>

Linkoski

thank you so much sir that was very useful in my code and helpful to understand more about the angles – Thorlay

@مهند عبد الجليل Thanks if you want you can accept it by checking the check mark on the side of the answer. – Linkoski

done sir :) sorry i didnt know that i have to do this when i get the answered iam new here – Thorlay

@مهند عبد الجليل You do not have to It is available to allow you to mark the accepted answer if you choose to. – Linkoski

For reference, this is the official and most updated documentation for math.atan2(): docs.python.org/3/library/math.html#math.atan2 – Infuscate

Answer 2

In general, the angle of a vector (x, y) can be calculated by math.atan2(y, x). The vector can be defined by 2 points (x1, y1) and (x2, y2) on a line. Therefore the angle of the line is math.atan2(y2-y1, x2-x1). Be aware that the y-axis needs to be reversed (-y respectively y1-y2) because the y-axis is generally pointing up but in the PyGame coordinate system the y-axis is pointing down. The unit of the angle in the Python math module is Radian, but the unit of the angle in PyGame functions like pygame.transform.rotate() is Degree. Hence the angle has to be converted from Radians to Degrees by math.degrees:

import math

def angle_of_vector(x, y):
    return math.degrees(math.atan2(-y, x))

def angle_of_line(x1, y1, x2, y2):
    return math.degrees(math.atan2(-(y2-y1), x2-x1))

This can be simplified by using the angle_to method of the pygame.math.Vector2 object. This method computes the angle between 2 vectors in the PyGame coordinate system in degrees. Therefore it is not necessary to reverse the y-axis and convert from radians to degrees. Just calculate the angle between the vector and (1, 0):

def angle_of_vector(x, y):
    return pygame.math.Vector2(x, y).angle_to((1, 0))

def angle_of_line(x1, y1, x2, y2):
    return angle_of_vector(x2-x1, y2-y1)

Minimale example:

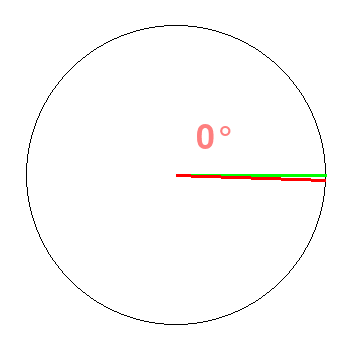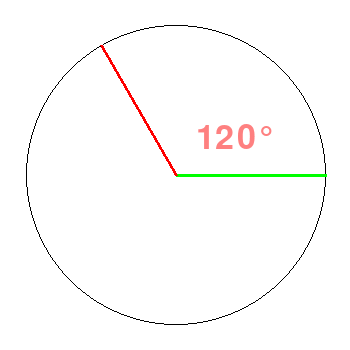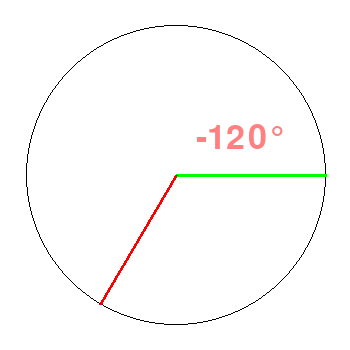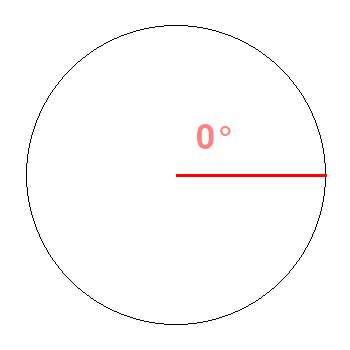
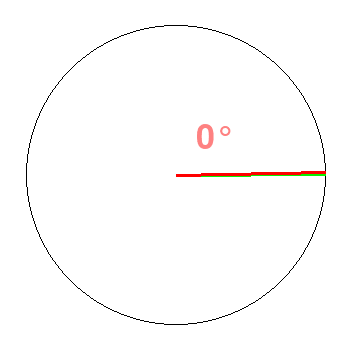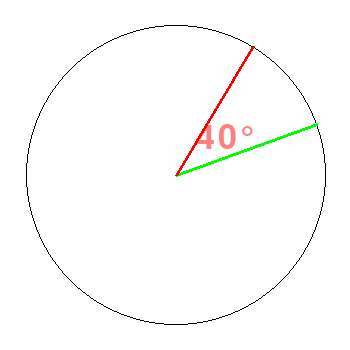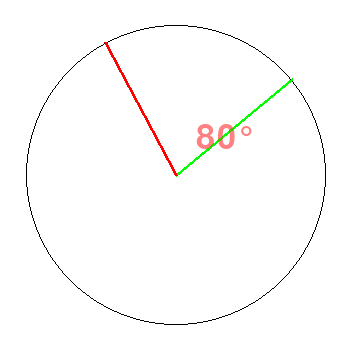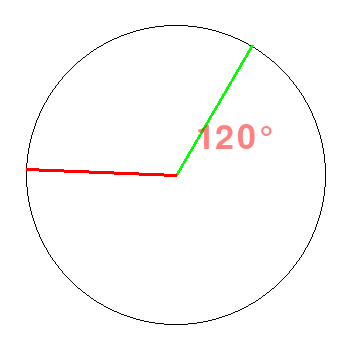
import pygame
import math

def angle_of_vector(x, y):
    #return math.degrees(math.atan2(-y, x))            # 1: with math.atan
    return pygame.math.Vector2(x, y).angle_to((1, 0))  # 2: with pygame.math.Vector2.angle_to
    
def angle_of_line(x1, y1, x2, y2):
    #return math.degrees(math.atan2(-y1-y2, x2-x1))    # 1: math.atan
    return angle_of_vector(x2-x1, y2-y1)               # 2: pygame.math.Vector2.angle_to
    
pygame.init()
window = pygame.display.set_mode((400, 400))
clock = pygame.time.Clock()
font = pygame.font.SysFont(None, 50)

angle = 0
radius = 150
vec = (radius, 0)

run = True
while run:
    clock.tick(60)
    for event in pygame.event.get():
        if event.type == pygame.QUIT:
            run = False

    cpt = window.get_rect().center
    pt = cpt[0] + vec[0], cpt[1] + vec[1]
    angle = angle_of_vector(*vec)

    window.fill((255, 255, 255))
    pygame.draw.circle(window, (0, 0, 0), cpt, radius, 1)
    pygame.draw.line(window, (0, 255, 0), cpt, (cpt[0] + radius, cpt[1]), 3)
    pygame.draw.line(window, (255, 0, 0), cpt, pt, 3)
    text_surf = font.render(str(round(angle/5)*5) + "°", True, (255, 0, 0))
    text_surf.set_alpha(127)
    window.blit(text_surf, text_surf.get_rect(bottomleft = (cpt[0]+20, cpt[1]-20)))
    pygame.display.flip()

    angle = (angle + 1) % 360
    vec = radius * math.cos(angle*math.pi/180), radius * -math.sin(angle*math.pi/180)

pygame.quit()
exit()

---

angle_to can be used to calculate the angle between 2 vectors or lines:

def angle_between_vectors(x1, y1, x2, y2):
    return pygame.math.Vector2(x1, y1).angle_to((x2, y2))

Minimal example:

import pygame
import math

def angle_between_vectors(x1, y1, x2, y2):
    return pygame.math.Vector2(x1, y1).angle_to((x2, y2))

def angle_of_vector(x, y):
    return pygame.math.Vector2(x, y).angle_to((1, 0))    
    
pygame.init()
window = pygame.display.set_mode((400, 400))
clock = pygame.time.Clock()
font = pygame.font.SysFont(None, 50)

angle = 0
radius = 150
vec1 = (radius, 0)
vec2 = (radius, 0)

run = True
while run:
    clock.tick(60)
    for event in pygame.event.get():
        if event.type == pygame.QUIT:
            run = False

    cpt = window.get_rect().center
    pt1 = cpt[0] + vec1[0], cpt[1] + vec1[1]
    pt2 = cpt[0] + vec2[0], cpt[1] + vec2[1]
    angle = angle_between_vectors(*vec2, *vec1)

    window.fill((255, 255, 255))
    pygame.draw.circle(window, (0, 0, 0), cpt, radius, 1)
    pygame.draw.line(window, (0, 255, 0), cpt, pt1, 3)
    pygame.draw.line(window, (255, 0, 0), cpt, pt2, 3)
    text_surf = font.render(str(round(angle/5)*5) + "°", True, (255, 0, 0))
    text_surf.set_alpha(127)
    window.blit(text_surf, text_surf.get_rect(bottomleft = (cpt[0]+20, cpt[1]-20)))
    pygame.display.flip()

    angle1 = (angle_of_vector(*vec1) + 1/3) % 360
    vec1 = radius * math.cos(angle1*math.pi/180), radius * -math.sin(angle1*math.pi/180)
    angle2 = (angle_of_vector(*vec2) + 1) % 360
    vec2 = radius * math.cos(angle2*math.pi/180), radius * -math.sin(angle2*math.pi/180)

pygame.quit()
exit()

Chuppah

Answer 3

Specifically for working with shapely linestring objects, assuming your object (two points) is of the form (min long, min lat, max long, max lat)

from math import atan2,degrees
line = #Your-LineString-Object
lineList = list(line.coords)

def AngleBtw2Points(pointA, pointB):
  changeInX = pointB[0] - pointA[0]
  changeInY = pointB[1] - pointA[1]
  return degrees(atan2(changeInY,changeInX)) #remove degrees if you want your answer in radians

AngleBtw2Points(lineList[0],lineList[1]) 

Throttle

Answer 4

I used following code.

import math

def get_angle(x1,y1,x2,y2):
    myradians = math.atan2(y1-y2, x1-x2)
    mydegrees = math.degrees(myradians)
    return mydegrees

# it should return -90 degree
print(get_angle(0,0,0,100))

Tepic

Answer 5

As one commenter already said, there is only an angle between three points or between two intersecting vectors, that can be derived from this threee points. I assume you want the angle, that the gun and the target (vector 1) and the X-Axis (vector 2) has. Here is a link to a page, that explains how to calculate that angle. http://www.euclideanspace.com/maths/algebra/vectors/angleBetween/index.htm

Python example:

import math

def angle(vector1, vector2):
    length1 = math.sqrt(vector1[0] * vector1[0] + vector1[1] * vector1[1])
    length2 = math.sqrt(vector2[0] * vector2[0] + vector2[1] * vector2[1])
    return math.acos((vector1[0] * vector2[0] + vector1[1] * vector2[1])/ (length1 * length2))

vector1 = [targetX - gunX, targetY - gunY] # Vector of aiming of the gun at the target
vector2 = [1,0] #vector of X-axis
print(angle(vector1, vector2))

Uraninite

Since the gun and the target are defined relative to implicit x, y axes then tangent = (y2-y1)/(x2-x1) would be used. This allows atan2 to be used. You do not need to calculate the (implicit) axis vector. – Linkoski

You right, atan2 is a possible shortcut. I showed the general mathematical formula for explanatory reasons. – Uraninite

In either case you do not need to use vector 2, since vector one allows you to do the calculations that you need. – Linkoski

Answer 6

You can just use the as_polar method of Pygame's Vector2 class which returns the polar coordinates of the vector (radius and polar angle (in degrees)).

So just subtract the first point vector from the second and call the as_polar method of the resulting vector.

import pygame as pg
from pygame.math import Vector2


pg.init()
screen = pg.display.set_mode((640, 480))
clock = pg.time.Clock()
BG_COLOR = pg.Color('gray12')

point = Vector2(320, 240)
mouse_pos = Vector2(0, 0)
radius, angle = (mouse_pos - point).as_polar()

done = False
while not done:
    for event in pg.event.get():
        if event.type == pg.QUIT:
            done = True
        elif event.type == pg.MOUSEMOTION:
            mouse_pos = event.pos
            radius, angle = (mouse_pos - point).as_polar()

    screen.fill(BG_COLOR)
    pg.draw.line(screen, (0, 100, 255), point, mouse_pos)
    pg.display.set_caption(f'radius: {radius:.2f} angle: {angle:.2f}')
    pg.display.flip()
    clock.tick(60)

Orifice

Answer 7

For anyone wanting a bit more information on this subject check out omnicalculator's break down of the subject: https://www.omnicalculator.com/math/angle-between-two-vectors

Extracted relevant information:

from math import acos, sqrt, degrees

# returns angle in radians between two points pt1, pt2 where pt1=(x1, y1) and pt2=(x2, y2)
angle = acos((x1 * x2 + y1 * y2)/(sqrt(x1**2 + y1**2) * sqrt(x2**2 + y2**2)))

# convert to degrees
deg_angle = degrees(angle)

Uterine