What is the number of filter in CNN?

Question

I am currently seeing the API of theano,

theano.tensor.nnet.conv2d(input, filters, input_shape=None, filter_shape=None, border_mode='valid', subsample=(1, 1), filter_flip=True, image_shape=None, **kwargs)

where the filter_shape is a tuple of (num_filter, num_channel, height, width), I am confusing about this because isn't that the number of filter decided by the stride while sliding the filter window on the image? How can I specify on filter number just like this? It would be reasonable to me if it is calculated by the parameter stride (if there is any).

Also, I am confused with the term feature map as well, is it the neurons at each layer? How about the batch size? How are they correlated?

Servile

"Number of filters are not arbitrary. They can be chosen either intuitively or empirically." Link – Kindliness

Answer 1

The number of filters is the number of neurons, since each neuron performs a different convolution on the input to the layer (more precisely, the neurons' input weights form convolution kernels).

A feature map is the result of applying a filter (thus, you have as many feature maps as filters), and its size is a result of window/kernel size of your filter and stride.

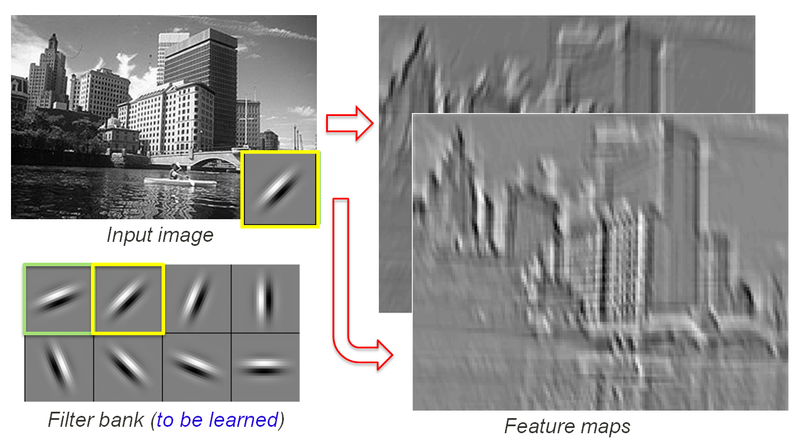
The following image was the best I could find to explain the concept at high level: Note that 2 different convolutional filters are applied to the input image, resulting in 2 different feature maps (the output of the filters). Each pixel of each feature map is an output of the convolutional layer.

For instance, if you have 28x28 input images and a convolutional layer with 20 7x7 filters and stride 1, you will get 20 22x22 feature maps at the output of this layer. Note that this is presented to the next layer as a volume with width = height = 22 and depth = num_channels = 20. You could use the same representation to train your CNN on RGB images such as the ones from the CIFAR10 dataset, which would be 32x32x3 volumes (convolution is applied only to the 2 spatial dimensions).

EDIT: There seems to be some confusion going on in the comments that I'd like to clarify. First, there are no neurons. Neurons are just a metaphor in neural networks. That said, "how many neurons are there in a convolutional layer" cannot be answered objectively, but relative to your view of the computations performed by the layer. In my view, a filter is a single neuron that sweeps through the image, providing different activations for each position. An entire feature map is produced by a single neuron/filter at multiple positions in my view. The commentors seem to have another view that is as valid as mine. They see each filter as a set of weights for a convolution operation, and one neuron for each attended position in the image, all sharing the same set of weights defined by the filter. Note that both views are functionally (and even fundamentally) the same, as they use the same parameters, computations, and produce the same results. Therefore, this is a non-issue.

Handknit

What about this sentence about choosing filter/kernel number: " In fact, to equalize computation at each layer, the product of the number of features and the number of pixel positions is typically picked to be roughly constant across layers" cited in deeplearning.net/tutorial/lenet.html. Could you give me an example? – Lorrinelorry

I think the OP is asking where your 20 filters came from. I mean why 20? – Wenonawenonah

I have that doubt too. Why 20? – Tolan

While this high level explanation is correct, I must clarify that number of filters != number of neurons per se. A group of neurons, each seeing part of the previous feature map (= the image for neurons of the first layer), and each applying the same weights form the whole "filter". Agreed, when coding you rarely need to know about this level of structure, but it doesn't change the fact that your first sentence is wrong. Nice explanation, though ! – Coating

Not really, if you just consider that each neuron is applied to various windows in sequence instead of having various copies (which is, in fact, more appropriate to the definition of convolution). The sentence is correct. – Handknit

"Number of filters are not arbitrary. They can be chosen either intuitively or empirically." Link – Kindliness

The accepted answer seems confusing and unclear. A convolutional layer apply the same kernel, moved by a stride to the input image. You dont't specify the number of neuron in the layer, this value is implicitly defined by the size of your kernel and your stride. Since neurons in a layer share the same weights, they are extracted the same feature. When you stack layers, you allow each layer to extract a different feature. The ensemble being your feature map. – Zippora

Answer 2

There is no correct answer as to what the best number of filters is. This strongly depends on the type and complexity of your (image) data. A suitable number of features is learnd from experience after working with similar types of datasets repeatedly over time. In general, the more features you want to capture (and are potentially available) in an image the higher the number of filters required in a CNN.

Fulminate

Answer 3

More than 0 and less than the number of parameters in each filter. For instance, if you have a 5x5 filter, 1 color channel (so, 5x5x1), then you should have less than 25 filters in that layer. The reason being is that if you have 25 or more filters, you have at least 1 filter per pixel. The filter bank should provide some lossy compression of the input, and if there are as many filters as parameters per filter, then it doesn't lose any data, it just massively overfits.

Azure

Answer 4

The number of filters is a hyper-parameter that can be tuned. The number of neurons in a convolutional layer equals to the size of the output of the layer. In the case of images, it's the size of the feature map.

Wellchosen

Answer 5

First you need to understand what filters actually do.

Every layer of filters is there to capture patterns. For example, the first layer of filters captures patterns like edges, corners, dots etc. Subsequent layers combine those patterns to make bigger patterns.

Convolutional Neural Networks are (usually) supervised methods for image/object recognition. This means that you need to train the CNN using a set of labelled images: this allows to optimize the weights of its convolutional filters, hence learning the filters shape themselsves, to minimize the error. Once you have decided the size of the filters, as much as the initialization of the filters is important to "guide" the learning, you can indeed initialize them to random values, and let the learning do the work.

Remember:

There is no definite rule as it depends on the case under consideration. For example, to classify images of digits from the MNIST database, which are 28 by 28 pixel black and white images, a good choice is to use 20 filters of size 9 by 9 (reference: MATLAB Deep Learning by P. Kim). This number of filters will be equal to the number of feature maps obtained In the first convolutional layer. Other types of images may require more or fewer feature maps depending on how structured the images are.

Excellent