Given a private key, is it possible to derive its public key?

Question

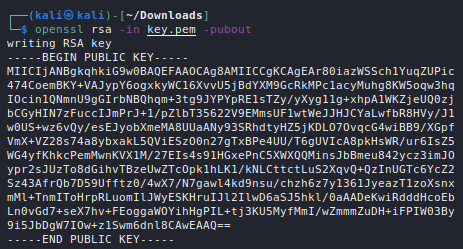
From whatever little I understand by reading various material, public-private key pair are the basis of asymmetric encryption and also something about choosing 2 prime numbers (which is roughly your private key) and multiplying them (which is roughly your public key). It appears to me that it is possible to generate a public key if you know the private key. Is it correct or I am mistaking something?

What made me more confusing was that it is not possible to serialize the RSA key to XML with only private key (using .NET class RSACryptoServiceProvider). Not sure whether this limitation is intentional or not!

Speciosity

It is possible. devopslife.io/recovering-ssh-public-key-with-the-private-key – Patiencepatient

Answer 1

That depends on the crypto system.

In RSA, we have (citing Wikipedia):

The public key consists of the modulus n and the public (or encryption) exponent e. The private key consists of the modulus n and the private (or decryption) exponent d which must be kept secret.

Now if we have n and d (the private key), we are only missing e for the public key. But e is often fairly small (less than three digits), or even fixed (a common value is 65537). In these cases getting the public key is trivial.

For Elliptic Curve Diffie-Hellman, the private key is d, and the public key dG (with G also public), so it's trivial as well.

Highkey

In RSA, if we know d and n, we can compute p and q such that pq = n. With this, d and e are each other's inverses modulo (p-1)(q-1). – Unanswerable

@Henno Bransma: How do you compute "p and q such that pq = n"? – Highkey

@HennoBrandsma Knowing d doesn't help you factor n, any more than knowing e does. – Divest

@HennoBrandsma that only works if you know both e and d (and n). Of course as sleske wrote form typical small es it's easy to guess them. But if you use RSA with large e, you won't be able to factor just from knowing d and n. In RSA e and d have symmetrical properties, but we usually choose small es for efficiently reasons. – Zilvia

I have in the past, written code to guess e given d and n. It tried about 10 possible values and quickly checked whether they were correct or not. (There is information available about the commonest rsa exponents used in the wild, and ten covers nearly everything.) – Hainaut

@MartinBonner: Yes, that's why I wrote in my answer "e is often small, or fixed". Feel free to submit an edit to make it clearer. – Highkey

What operation between "d" and "G" does "dG" refer to? Generally that means multiplication, but you said G is public, so it can't be multiplication or else you could get the private key through simple division. – Florentinoflorenza

@flarn2006: It is multiplication - but not the type you learn in school, but Elliptic curve point multiplication (en.wikipedia.org/wiki/Elliptic_curve_point_multiplication ). Unlike normal multiplication, "division" is not possible on an elliptic curve. – Highkey

I'd be curious to know which crypto systems do not allow the public key to be derived from the private key. – Caprification

Answer 2

In most asymmetrical crypto system implementation, the only fact that is ensured is that you cannot find the private key from the public key. The other way round, finding the public key from the private key is trivial in most case.

For instance, in RSA, you can create public key from private key with:

openssl rsa -in private.pem -pubout -out public.pem

What is misleading is the terminology: "private key" refers to 2 different concepts whether you are speaking of the theory, or wether you are speaking of practical implementation:

• The theoretical private key is the couple (d, n) which shares perfect symmetrical (mathematical) relation with (e, n). If you are comparing these, one cannot be computed from the other.
• The practical private key (as in openssl implementation for example), refers to a file containing (d, n) but also several important intermediate values for decoding speed purpose. In addition to that, the theoretically "unknown" part of the public key e is often fixed to common values by convention (which is 0x10001 by default in openssl and albeit it can be changed, it is strongly recommended to stick to only very specific values). So deducing the public key (e, n) from the private key is trivial for more than one reason.

Starling

In the PKCS#8 you don't only get the values to perform the Chinese Remainder Theorem (CRT) calculations but the public exponent as well. So for OpenSSL private keys you don't have to deduce anything. If you don't want to specify the public key exponent during key pair generation, then openssl defines the -f4 argument to use the fourth number of Fermat, which is indeed 0x010001 (a prime number with just two bits set to 1 for efficiency reasons, as it is easy to multiply with the value 0) – Troopship

Re openssl: library has long supported any reasonable pubexpt. Traditional commandline genrsa does default to -f4 = 65537 and also supports -3 = 3 (see crypto.SX for several Qs on whether e=3 is good, bad, or ugly); since 1.0.0 release in 2010 commandline genpkey -algorithm RSA -pkeyopt rsa_keygen_pubexp:$value supports any reasonable value. – Parris

Answer 3

It depends on the algorithm, and what you mean by "private key".

RSA private keys are often stored in their "Chinese Remainder Theorem" form. For example, the RSAPrivateKey structure defined in PKCS #1 and re-used by many other crypto standards take this form. This form includes the two secret numbers often denoted p and q, from which the totient is computed. With totient and the private exponent, the public exponent is quickly computed.

In any case, most RSA key pairs use 65537 as the public exponent, and the modulus is always carried as part of the private key.

Divest

Answer 4

There is a misconception on what the private key is. The private key is just the (d,n) pair and, given only that, it is infeasible to generate the public key from it unless you can assume that the public exponent is 65537, which is the case on almost all rsa keys.

If, for any reason, the public exponent is a larger number you cannot create the public key from the private one.

That said, the value stored as "private key" to pem files is not just the private key, but also contains the prime factors (among other things) and, therefore, it's easy to generate the public key from it.

Ibbison

Answer 5

In ANY public key crypto system the public key is mathematically related to the private key. It's very simple.

The public key is derived from the private key at generation time, and with the private key at any point in the future it is possible to re-derive the public key easily.

It is not feasible to go the other way. Given a public key it is not easy to derive the private key. That's why we can safely share public keys with other people. If you have enough time/CPU cycles you could brute force it but it's probably easier to wait for a mathematical attack on the key.

Signorina

You need the totient to easily re-derive the public key, but the private key is only the private exponent and the modulus. Deriving the totient from that information requires factoring large numbers, and no fast algorithm is known. – Divest

Answer 6

For the specific case of OpenSSH and ssh-keygen, yes you can:

ssh-keygen -y

This option will read a private OpenSSH format file and print an public key to stdout.

---

Generally, it depends on the algorithm and what you label the private key. However, any sensible implementation will include the complete information (public and private keys) in the secret file.

Jaan

Answer 7

Yes it is possible to fetch the public key using the private key. It could be done using openssl. Please refer the below command to get the public key using the private key.

openssl rsa -in privatekey.pem  -pubout 

Please refer to the screenshot:

Fatally

Answer 8

Yes with access to the private key the public key can be generated

Tetrahedral

Is it (your answer) applicable to RSA generally or specific to Microsoft CryptoAPI implementation (and the way it serializes the key to/from XML)? – Speciosity

Actually this is not true either - they are both products of complex calculations. – Stymie

The question was originally asked in principle, hence the answer is in princple. I don't know the internals of .NET encryption, however private keys may store the originating p and q. One should assume that a public key is derivable from a private key. – Tetrahedral

Answer 9

public key is modulus N (and public exponent e, usually 65537), private key is given by the two primes p, q (and private exponent d, sometimes also CRT parts d_p, d_q for speedup) essentially you have N=pq and ed=1 mod ((p-1)(q-1)), you can also compute d_p and d_q using CRT given private key, computation of public key modulus is "boring" multiplication and public exponent is in specification or computed using extended euclid algorithm if standard e was not good enough. given public key, computation of private key requires either finding d (RSA problem) or p,q (factoring, see number field sieve for best algo to do this). These problems are shown to be equivalent under reasonable conditions [Breaking RSA Generically is Equivalent to Factoring, D. Aggarwal and U. Maurer, 2008]

Pelorus

Answer 10

It is theoretically possible but for large keys computationally infeasible.

Tychonn