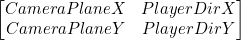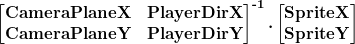What is the math behind billboard sprite drawing? (inverse matrix)

Question

I am following "Raycasting Tutorial" in this site Rayacasting Tutorial, in order to create a 3D perspective in a 2D map similar to an old game known as Wolfenstein_3D.

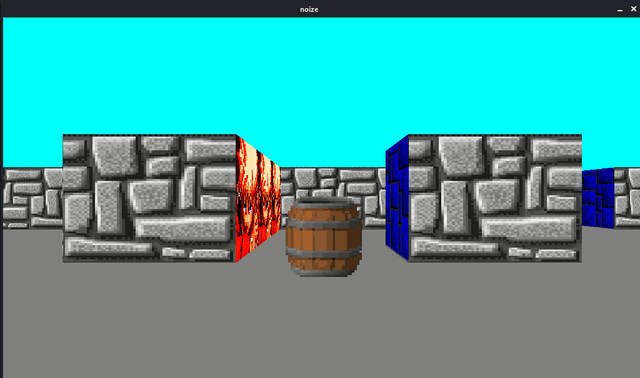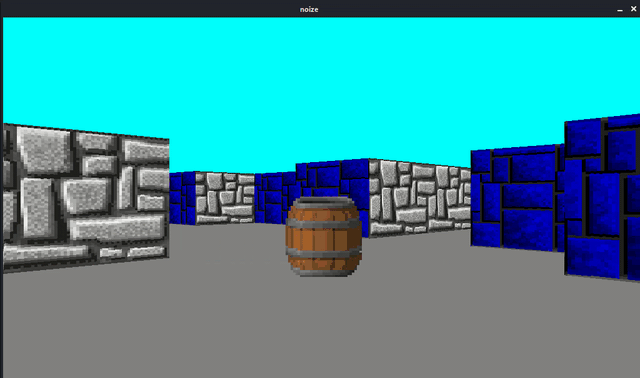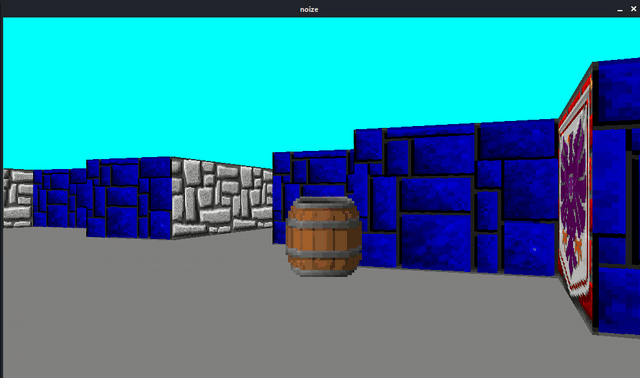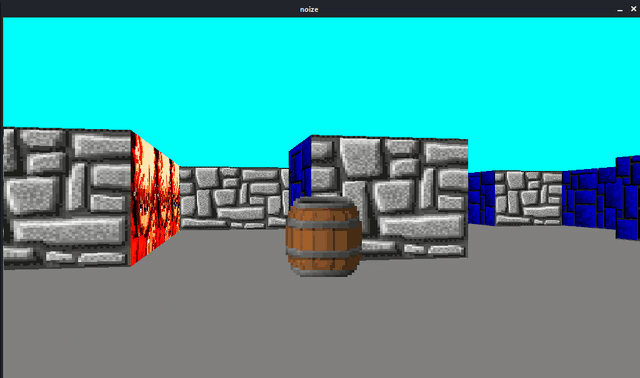
Here is the result so far as shown in this image:

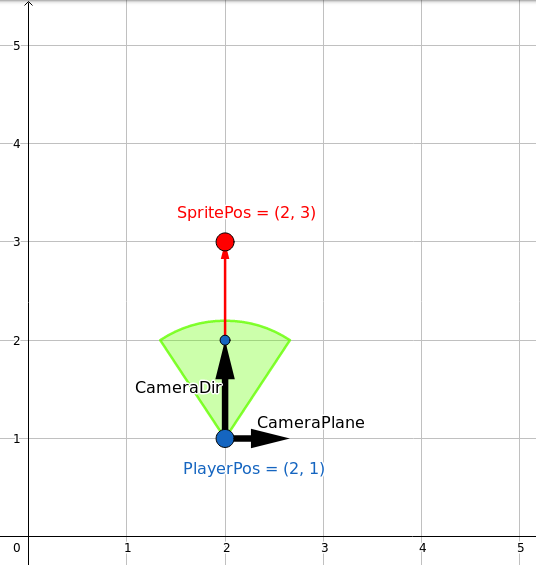
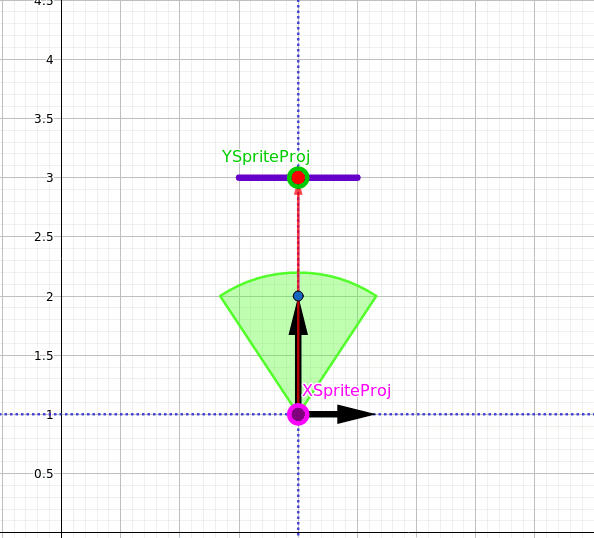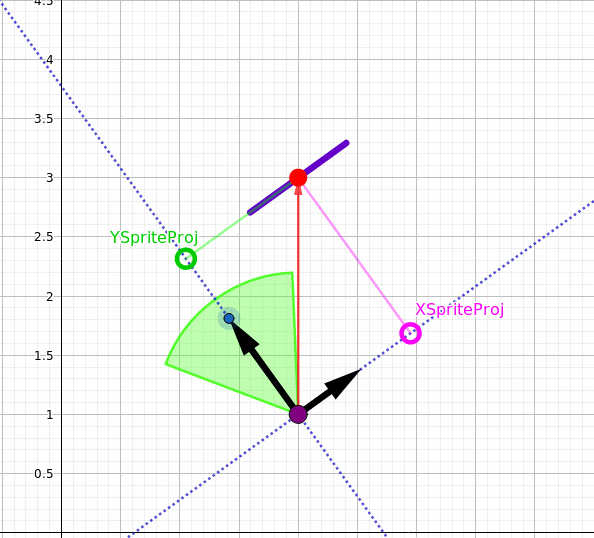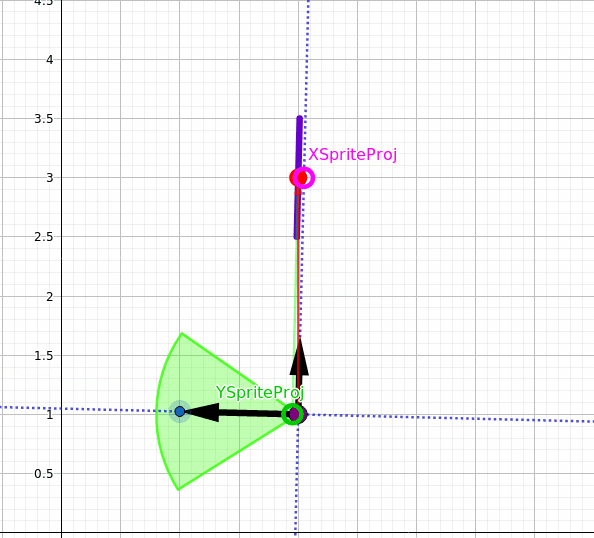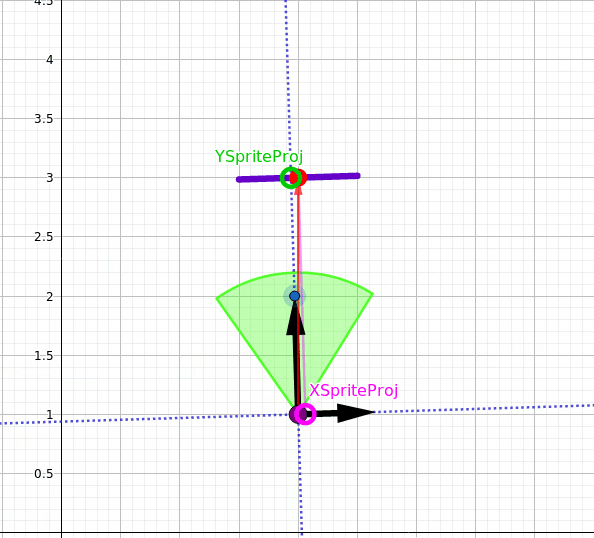
What I am confused about is the math behind rendering a billboard 2d sprite which is always facing the camera direction.

Here is the billboard 2d sprite how it looks like:

I followed the tutorial about sprite rendering, that you can find it here Draw_Sprite, and I managed to display the billboard sprite in my scene as you can see in the first image, and in the tutorial, they used the inverse matrix, they multiplied the relative position of the sprite with the inverse of the camera matrix.

the relative position of the sprite is combined with 2 coordinates since we are working on a 2d map and it's as follows:

(Disable the dark theme if you want to see a clear image)

and the camera matrix is as follows:

in the tutorial as I mentioned earlier they multiplied the relative position of the sprite with the inverse of the camera matrix as shown below:

But I don't understand how it works, why we need to multiply the inverse of the camera matrix with the matrix of our sprite, I want to understand the logic behind it, How this formula makes the sprite rotate to be always facing the camera direction ?! I am still new in game development.

Endolymph

by multiplying inverse matrix you cancel previous rotation ... its unrotating back. Its weird to use matrices for 2D ray caster ... see Ray Casting with different height size as you can see no matrices are used ... – Tepic

@Tepic Yeah, it's just in this tutorial which I am following works with vectors and camera instead of Euclidean angles. – Endolymph

also if your matrices are only 2x2 and holding only rotation then transpose is the same as inverse so you do not need to implement complicated/slow inverse of matrix ... Transpose is easy just swap the 2 elements on second diagonal (bottom left <-> top right) – Tepic

@Tepic Yeah, it's faster this way I didn't know this information before, Thank you so much. – Endolymph

Answer 1

First some math background for this:

2x2 matrix for 2D holds just rotation matrix. That means:

mat2 m;    // rotation matrix
vec2 a,b;  // 2D points

b = m*a;   // rotates a by m and stores into b

If you multiply by inverse:

mat2 n;
n = inverse(m);
b = n*b;

You obtained original position a because multiplying inverse and direct matrix is unit matrix:

           b =            m*a 
inverse(m)*b = inverse(m)*m*a 
inverse(m)*b =              a 

However using matrices for 2D ray caster is highly unusual as its complicates things. See:

• Ray Casting with different height size.

Also using just rotational matrix means you have to offset/translate on your own either before or after rotation. So my bet you are doing in code something like this:

a = rotation_matrix*a;
a += translation;
a = Inverse(rotation_matrix)*a;

As I mentioned in the comments for purely rotational matrices the Transpose function is the same as Its inverse so for 2D:

m = a0 a1    inverse(m) = transpose(m) = a0 a2
    a2 a3                                a1 a3

For more info about matrices take a look at:

• Understanding 4x4 homogenous transform matrices

There are more possible notations of doing this math (using direct or inverse matrices, using row/column major order, multiplying order etc ... which might slightly change the equations).

However your matrix description does not seem right. It should be:

| camerax.x cameray.x |
| camerax.y cameray.y |

So basically the 2 direction vectors (one for x axis and one for y axis of camera/player) in world coordinates (but the camera plane normal is parallel to the other direction so its the same ... just confusing a lot)

Now this is how I see it:

The player is your camera so what you need os to convert the sprite world postion sw into player coordinates sp. And then just render the sprite parallel to player xz plane (or any other if your axises are configured differently).

so let the mp be player rotation matrix and pp players world position then:

sp = mp*(sw-pp)

is the sprite converted into player coordinates. However depending on your engine you might need a fake wall parallel to players xz in world coordinates instead. So the wall would be at:

sprite_wall_vertexes = sw (+/-) (inverse(mp)*sprite_half_size)

Tepic

So as I understand from your explanation is that we need to convert the sprite world position (SpritePosX, SpritePosY) into the player coordinates (PlayerPosX, PlayerPosY), then we can know our SpriteX and SpriteY new positions which the player position is like the origin. and SpriteY is the projection in the direction of the player and SpriteX is the projection in the camera plane. correct me if I am wrong – Endolymph

and I see that you multiplied (sw - pp) with the player rotation matrix, but in the tutorial, they multiplied it with the inverse, I didn't get it, I am bad at math a little bit. – Endolymph

@Holysemicolon it depends on the notations used ... it might be direct or inverse matrix. Which depends on the combination of if the matrix itself is direct or inverse, if the basis vectors are in columns or rows, if you multiply vector or transposed vector etc ... Nice example is OpenGL vs DirectX they usually use different matrix layout so what is direct in GL is Inverse in DX and vice versa – Tepic

I posted an answer to explain more about multiplying with inverse matrix, I hope you check my explanation and see if there is any unlogic thing, to remove it from my answer, of course, if you have enough time, and I appreciate that so much. – Endolymph

Hey, any idea how to get the other axis? Like, we get X in camera plane and distance from the camera but is there a way to get Y in the camera plane? – Diocletian

@Diocletian in 2D its always just 90 degree rotation of the other axis ... so for any direction vector just swap the (x,y) and negate one so either (-y,x) or (y,-x) which depends on your coordinate systems notation (its just the difference between rotating CW or CCW ...) However beware this works only on uniformly scaled spaces (where unit on x is the same as unit on y) – Tepic

Ah, awesome! Thank you! – Diocletian

Answer 2

Thanks to @Spektre I was able to understand why we multiplied the relative position of the sprite with the inverse of the camera matrix, I just wanted to add more information and explanation.

Well, first of all, let's see our player positions in the below image:

As we can see the PlayerPos is (2,1) and the SpritePos is (2,3), the first thing we must do is to know the position of our sprite according to the Player Position, so:

SpriteX = SpritePosX - PlayerPosX = 2 - 2 = 0
SpriteY = SpritePosY - PlayerPosY = 3 - 1 = 2

then our sprite position according to the player position is (0,2), which is represented by the red vector in the above image.

But what will happen if we didn't multiply the red vector coordinates with the inverse of the camera matrix?

then we will use the real distance from the player position to the sprite position, and when the camera view will rotate, the red vector will be rotated with it, so when you will draw your sprite it will be always perpendicular with the CameraPlane which we don't want it to happen.

here is how it will look like in the diagram:

and here is how it will look like in the game:

Now, what will happen if we multiply the relative position of the sprite (red vector) with the inverse of the camera matrix?

As you know and as @Spektre mentioned in the comment section,

"by multiplying inverse matrix you cancel previous rotation ... its 'unrotating' back"

, so when we will multiply the relative position of the sprite (red vector) with the inverse of the camera matrix, the rotation of the camera/player will not affect the red vector and it will stay still, and we will have new coordinates of our red vector according to the camera view.

Here is what will happen in the diagram if we multiplied the red vector with the inverse of the camera matrix:

and in the game:

Endolymph

only one thing the vector you named camera plane is just single axis of the camera screen (usually x) ... planes are described by normal vectors which in this case would be your camera direction so your naming is confusing that is why I chose in my answer to call the vectors x,y where camera view direction is y and screen is in plane xz ... In 3D its usual to have z as viewing direction and screen in xy plane however in 2D its more didactical to have xz as palne so you deal just with x,y coordinates on the map plane... +1 nice GIFs btw – Tepic

@Tepic Thank you so much for your response, here is the site that I used to create the diagram just in case someone wants to work with it. geogebra.org/calculator – Endolymph