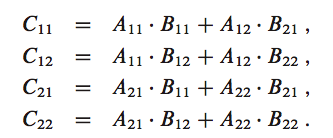Matrix Multiplication using Divide and Conquer, Time Complexity

Question

I understand that the algorithm uses 8 multiplications and 4 additions with time-complexity:

The multiplication is done on every n/2 * n/2 matrices. I have few questions on this :

1. Does every n * nmatrix finally gets reduced to n=1 size by performing T(n/2)? If so returning a11*b11 seems meaningless like returning 1*6 for a11*b11 for the below matrix:

Then the base case should be n==2 performing the else part since the below operation seems legit.

2. Why is the addition part taking 0(n^2) ? I mean, we are totally not dealing with matrix additions but mere numbers because every matrix is reduced to 2 * 2like below:

So the addition part should contribute just 4? (why 0(n^2)?)

Intolerance

Answer 1

If I understood the question correctly, the parts can be answered as follows.

1. In fact, all matrices get finally reduced to 1*1 matrices; this should not be too surprising, as the elementary definition of matrix multiplication is ultimately defined in terms of the multiplication of the underlying ring.

2. The addition part has complexity 0(n^2) on every level of the recursion as the addition is performed on the results of the recursive evaluation of the multiplication.

Verbenaceous

This is not Strassen's algorithm. Its just plain divide and conquer technique. – Intolerance

Answer 2

1)The matrix does get reduced to a 1*1 matrices in the end. But it does not matter,you can even put a base case for n==2 and it still will be O(1) time as multiplying a 2*2 matrix still takes constant time and the complexity will still remain the same.

2) The addition part should have complexity O(n^2) since every subproblem has (n^2)/4 elements and there are 4 such subproblems which means your are really performing n^2 operations which results in O(n^2) complexity.

Inlaid

Answer 3

Just seeing the algorithm it may not be clear why addition step is taking theta(n^2) time. I also have same confusion that addition should take constant time. With 2*2 matrix in addMatrices() method if we do following change

C[rowC][columnC] = A[0][0] + B[0][0];

then also it give same result.

But once we take 4*4 matrix then can see there will be some addMatrices() method call happening from call stack which is adding more than one element from matrices A and B. That is why addition is needed to be run inside loop.

After implementing the program it is much easier to understand. I have tried to explain, for details please refer method comments.

package matrix;

/***
 * Square Matrix multiplication(2^x) using divide and conquer technique
 * 
 * @author kmandal
 *
 */
public class MatrixMultiplication {

    public static void main(String[] args) {
        int[][] A = { { 1, 2 }, { 3, 4 } };
        int[][] B = { { 5, 6 }, { 7, 8 } };
        int C[][] = squareMatrixMultiplyRecursive(A, B);

        for (int i = 0; i < C.length; i++) {
            for (int j = 0; j < C.length; j++) {
                System.out.print(C[i][j] + "    ");
            }
            System.out.println();
        }
    }

    private static int[][] squareMatrixMultiplyRecursive(int[][] A, int[][] B) {
        return squareMatrixMultiplicationDNC(A, B, 0, 0, 0, 0, A.length);
    }

    /**
     * <pre>
     * Let A and B are 2 square matrices with dimension 2^x
     * A = [
     *      A00     A01
     *      A10     A11
     *      ]
     * ,
     * B = [
     *      B00     B01
     *      B10     B11
     *      ]
     * 
     * C be another matrix stores the result of multiplication of A and B.
     * 
     *  C = A.B;
     *  
     *  C = [
     *      C00     C01
     *      C10     C11
     *      ]
     *  
     *  where
     *  for C00 calculation, elements in 0th row of A and 0th column of B considered
     *  C00 = A00*B00+A01*B10;  
     *  
     *  for C01 calculation, elements in 0th row of A and 1st column of B considered
     *  C01 = A00*B01+A01*B11; 
     *  
     *  for C10 calculation, elements in 1st row of A and 0th column of B considered
     *  C10 = A10*B00+A11*B10; 
     *  
     *  for C11 calculation, elements in 1st row of A and 1st column of B considered
     *  C11 = A10*B01+A11*B11;
     * 
     * Here we are using index based calculation, 
     * hence time complexity for index calculation is Theta(1). 
     * 
     * We have divided the problem into 8 sub-problems with size n/2.
     * Hence the recurrence for this divide part is: 8T(n/2).
     * 
     * Additionally we need to consider the cost of matrix addition step, 
     * which is Theta(n^2). For more details refer addMatrices() method.
     * 
     * Hence the recurrence relation become 
     * T(n) = Theta(1) + 8T(n/2)+ Theta(n^2);
     * 
     * Applying Master theorem, 
     * the time complexity of this algorithm become O(n^3)
     * </pre>
     * 
     * @param A
     * @param B
     * @param rowA
     * @param columnA
     * @param rowB
     * @param columnB
     * @param size
     * @return
     */
    private static int[][] squareMatrixMultiplicationDNC(int[][] A, int[][] B,
            int rowA, int columnA, int rowB, int columnB, int size) {
        int[][] C = new int[size][size];
        if (size == 1) {
            C[0][0] = A[rowA][columnA] * B[rowB][columnB];
        } else {
            int newSize = size / 2;
            // calculate C00 = A00*B00+A01*B10;
            addMatrices(
                    C,
                    squareMatrixMultiplicationDNC(A, B, rowA, columnA, rowB,
                            columnB, newSize),
                    squareMatrixMultiplicationDNC(A, B, rowA,
                            columnA + newSize, rowB + newSize, columnB, newSize),
                    0, 0);
            // calculate C01 = A00*B01+A01*B11;
            addMatrices(
                    C,
                    squareMatrixMultiplicationDNC(A, B, rowA, columnA, rowB,
                            columnB + newSize, newSize),
                    squareMatrixMultiplicationDNC(A, B, rowA,
                            columnA + newSize, rowB + newSize, columnB
                                    + newSize, newSize), 0, newSize);
            // calculate C10 = A10*B00+A11*B10;
            addMatrices(
                    C,
                    squareMatrixMultiplicationDNC(A, B, rowA + newSize,
                            columnA, rowB, columnB, newSize),
                    squareMatrixMultiplicationDNC(A, B, rowA + newSize, columnA
                            + newSize, rowB + newSize, columnB, newSize),
                    newSize, 0);
            // calculate C11 = A10*B01+A11*B11;
            addMatrices(
                    C,
                    squareMatrixMultiplicationDNC(A, B, rowA + newSize,
                            columnA, rowB, columnB + newSize, newSize),
                    squareMatrixMultiplicationDNC(A, B, rowA + newSize, columnA
                            + newSize, rowB + newSize, columnB + newSize,
                            newSize), newSize, newSize);

        }
        return C;
    }

    /**
     * Matrix I represented by 2 dimensional array hence for addition of 2
     * matrices, need to fetch same element from both the matrices and then
     * add them. Traversing 2D array mean need to access elements by row and
     * column index thus need to loop inside loop. Hence time complexity of
     * addition is Theta(n^2)
     * 
     * @param C
     * @param A
     * @param B
     * @param rowC
     * @param columnC
     */
    private static void addMatrices(int[][] C, int[][] A, int[][] B, int rowC,
            int columnC) {
        int n = A.length;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                C[i + rowC][j + columnC] = A[i][j] + B[i][j];
            }
        }
    }
}

Output:
19    22    
43    50  

Introvert