The discrepancy is mainly due to the differing pdfs.
Python
In python st.pareto.fit() uses a Pareto distribution defined via this pdf:
![enter image description here]()
import scipy.stats as st
data = [2457.145, 1399.034, 20000.0, 476743.9, 24059.6, 28862.8]
print(st.pareto.fit(data, floc = 0, scale = 1))
# (0.4019785013487883, 0, 1399.0339889072732)
R
Whereas your R code is using a Pareto with this pdf:
![enter image description here]()
library(fitdistrplus)
library(actuar)
data <- c(2457.145, 1399.034, 20000.0, 476743.9, 24059.6, 28862.8)
fitdist(data, 'pareto', "mle")$estimate
# shape scale
# 0.760164 10066.274196
Make R Mirror Python
To get R to use the same distribution as st.pareto.fit() use actuar::dpareto1():
library(fitdistrplus)
library(actuar)
data <- c(2457.145, 1399.034, 20000.0, 476743.9, 24059.6, 28862.8)
fitdist(data, 'pareto1', "mle")$estimate
# shape min
# 0.4028921 1399.0284977
Make Python Mirror R
And here is one approach to approximate your R code in Python:
import numpy as np
from scipy.optimize import minimize
def dpareto(x, shape, scale):
return shape * scale**shape / (x + scale)**(shape + 1)
def negloglik(x):
data = [2457.145, 1399.034, 20000.0, 476743.9, 24059.6, 28862.8]
return -np.sum([np.log(dpareto(i, x[0], x[1])) for i in data])
res = minimize(negloglik, (1, 1), method='Nelder-Mead', tol=2.220446e-16)
print(res.x)
# [7.60082820e-01 1.00691719e+04]

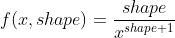
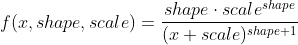
fitdist? – Revolutionactuarandfitdistrpluslibraries – Rena