Cut a shapely polygon into N equally sized polygons

Question

I have a Shapely polygon. I want to cut these polygon into n polygons, which all have more-or-less equally sized areas. Equally sized would be best, but an approximation would be okay too.

I have tried to use the two methods described here, which both are a step in the right direction by not what I need. Both don't allow for a target n

I looked into voronoi, with which I am largely unfamiliar. The resulting shapes this analysis gives would be ideal, but it requires points, not a shape as input.

Sartain

Answer 1

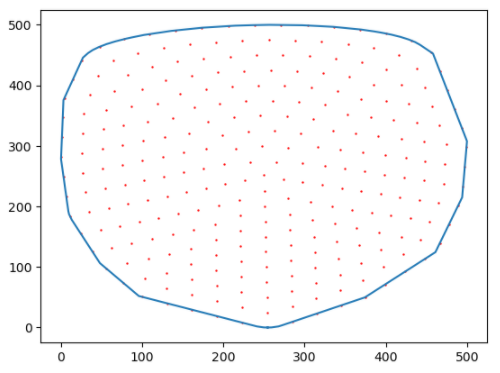
This is the best I could manage. It does not result in equal surface area per polygon, but it turned out to work for what I needed. This populates a shape with a specific number of points (if the parameters are kept constant, the number of points will be too). Then the points are converted to a voronoi, which was then turned into triangles.

from shapely import affinity
from shapely.geometry.multipolygon import MultiPolygon
from scipy.spatial import Voronoi

# Voronoi doesn't work properly with points below (0,0) so set lowest point to (0,0)
shape = affinity.translate(shape, -shape_a.bounds[0], -shape_a.bounds[1])

points = shape_to_points(shape)

vor = points_to_voronoi(points)

triangles = MultiPolygon(triangulate(MultiLineString(vor)))



def shape_to_points(shape, num = 10, smaller_versions = 10):
    points = []

    # Take the shape, shrink it by a factor (first iteration factor=1), and then 
    # take points around the contours
    for shrink_factor in range(0,smaller_versions,1):
        # calculate the shrinking factor
        shrink_factor = smaller_versions - shrink_factor
        shrink_factor = shrink_factor / float(smaller_versions)
        # actually shrink - first iteration it remains at 1:1
        smaller_shape = affinity.scale(shape, shrink_factor, shrink_factor)
        # Interpolate numbers around the boundary of the shape
        for i in range(0,int(num*shrink_factor),1):
            i = i / int(num*shrink_factor)
            x,y =  smaller_shape.interpolate(i, normalized=True).xy
            points.append( (x[0],y[0]))
    
    # add the origin
    x,y = smaller_shape.centroid.xy
    points.append( (x[0], y[0]) ) # near, but usually not add (0,0)
    
    points = np.array(points)
    return points


def points_to_voronoi(points):
    vor = Voronoi(points)
    vertices = [ x for x in vor.ridge_vertices if -1 not in x]
    # For some reason, some vertices were seen as super, super long. Probably also infinite lines, so take them out
    lines = [ LineString(vor.vertices[x]) for x in vertices if not vor.vertices[x].max() > 50000]
    return MultiLineString(lines)

This is the input shape:

This is after shape_to_points:

This is after points_to_voronoi

And then we can triangulate the voronoi:

Sartain

Hi, you are using some functions in your answer which are not seen how they are imported? Could you please add the imports? Thank you so much – Adapa

Heya. I have added my best guess. I don't have access to a machine to test right now. Please let me know if it doesn't work and I'll remove it from the answer. – Sartain

Hi again, thanks Mitchell. One more question: I have a type: Polygon and the code crashes. What type is the Shape? Can I convert one another? – Adapa

Also, how did you plot? – Adapa

Answer 2

Just combining the response and basic polyfill docs provided by @user3496060 (very helpful for me, thank you), here's a simple function.

And here's a great notebook from the h3 repo. Check out the "Census Polygon to Hex" section for how they use polyfill().

    def h3_fill_shapely_poly(poly = shape, res = 10):
        """
        inputs:
               - poly: must be a shapely Polygon, cannot be any other shapely object
               - res: resolution (higher means more specific zoom)
        output:
               - h3_fill: a Python set() object, generated by polypill
        """
        coordinates = [[i[0], i[1]] for i in poly.exterior.coords]
        geo_json = {
                "type": "Polygon",
                "coordinates": [coordinates]
        }
        h3_fill = h3.polyfill(geo_json, res, geo_json_conformant=False)
        print(f'h3_fill =\n{type(h3_fill), h3_fill}')
        return h3_fill

Sherrillsherrington

Answer 3

Another out-of-the-box option out there is the h3 polyfill function. Basically any repeating structure would work (triangle, square, hex), but Uber's library uses hexes so you're stuck with that unless you write a module to do the same thing with one of the other shapes. You still have the issue with "n" not being specified directly though (only indirectly through the discrete zoom level options).

polyfill

Halfmoon