Accuracy while learning MNIST database is very low (0.2)

Question

I am developing my ANN from scratch which is supposed to classify MNIST database of handwritten digits (0-9). My feed-forward fully connected ANN has to be composed of:

1. One input layer, with 28x28 = 784 nodes (that is, features of each image)
2. One hidden layer, with any number of neurons (shallow network)
3. One output layer, with 10 nodes (one for each digit)

and has to compute gradient w.r.t. weights and bias thanks to backpropagation algorithm and, finally, it should learn exploiting gradient descent with momentum algorithm.

The loss function is: cross_entropy on "softmaxed" network's outputs, since the task is about classification.

Each hidden neuron is activated by the same activation function, I've chosen the sigmoid; meanwhile the output's neurons are activated by the identity function.

The dataset has been divided into:

1. 60.000 training pairs (image, label) - for the training
2. 5000 validation pairs (image, label) - for evaluation and select the network which minimize the validation loss
3. 5000 testing pairs (image, label) - for testing the model picked using new metrics such as accuracy

The data has been shuffled invoking sklearn.utils.shuffle method.

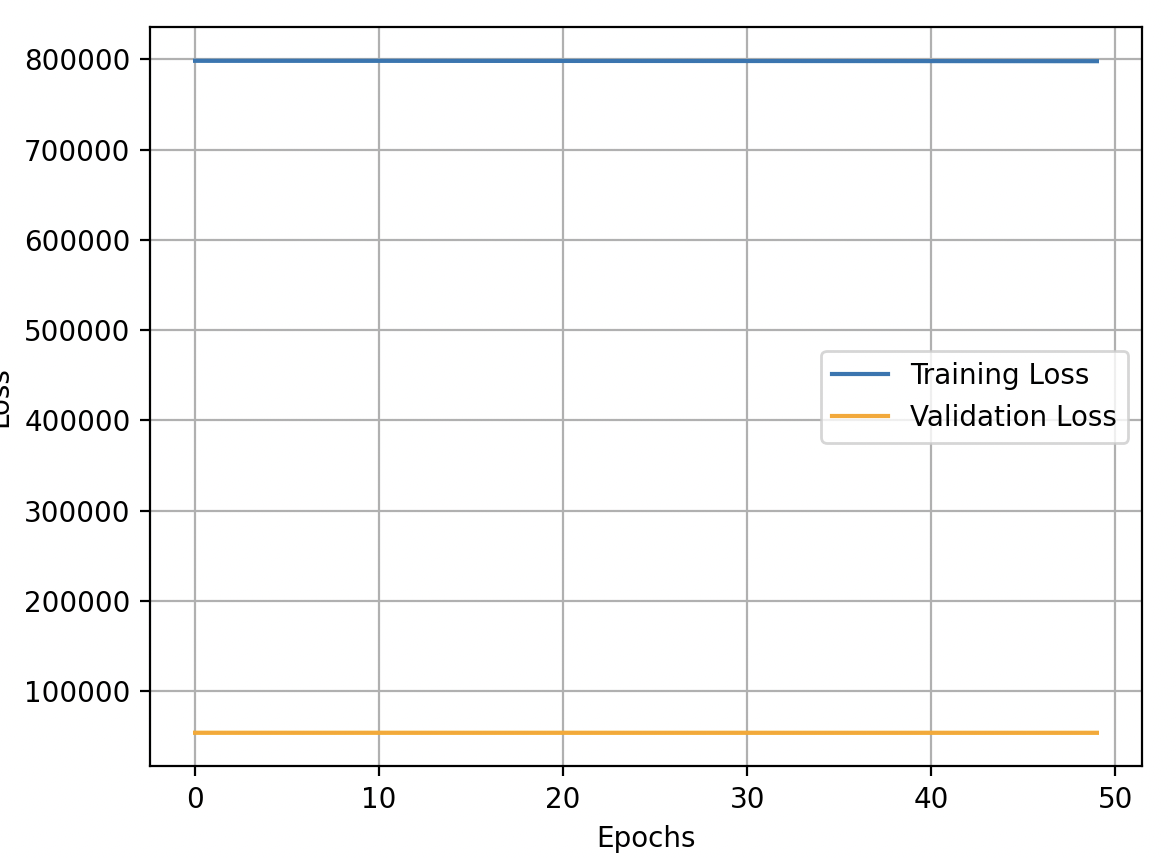
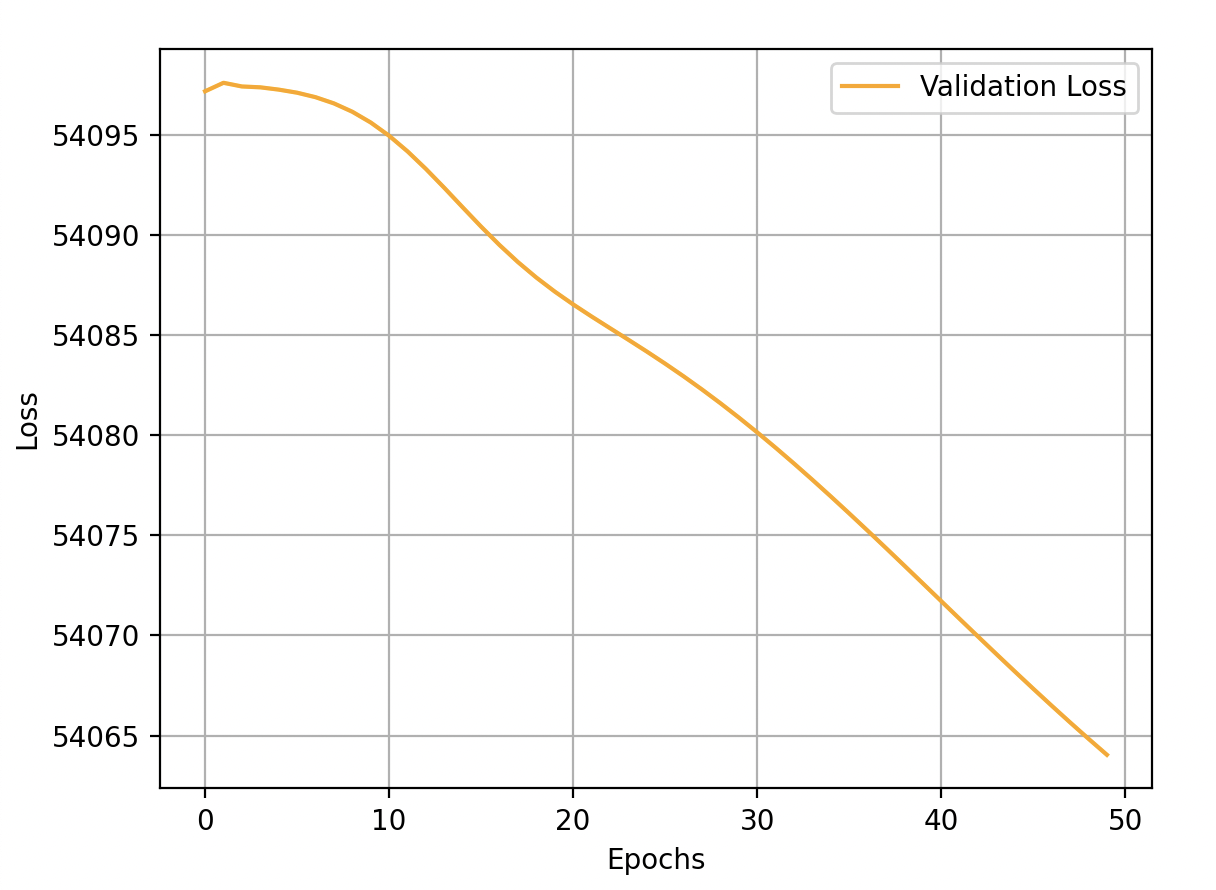
These are my net's performance about training loss, validation loss and validation accuracy:

E(0) on TrS is: 798288.7537714319  on VS is: 54096.50409967187  Accuracy: 12.1 %
E(1) on TrS is: 798261.8584179751  on VS is: 54097.23663558976  Accuracy: 12.1 %
...
E(8) on TrS is: 798252.1191081362  on VS is: 54095.5016235736  Accuracy: 12.1 %
...
E(17) on TrS is: 798165.2674011206  on VS is: 54087.2823473459  Accuracy: 12.8 %
E(18) on TrS is: 798155.0888987815  on VS is: 54086.454077456074  Accuracy: 13.22 %
...
E(32) on TrS is: 798042.8283810444  on VS is: 54076.35518400717  Accuracy: 19.0 %
E(33) on TrS is: 798033.2512910366  on VS is: 54075.482037626025  Accuracy: 19.36 %
E(34) on TrS is: 798023.431899881  on VS is: 54074.591145985265  Accuracy: 19.64 %
E(35) on TrS is: 798013.4023181734  on VS is: 54073.685418577166  Accuracy: 19.759999999999998 %
E(36) on TrS is: 798003.1960815473  on VS is: 54072.76783050559  Accuracy: 20.080000000000002 %
...
E(47) on TrS is: 797888.8213232228  on VS is: 54062.70342708315  Accuracy: 21.22 %
E(48) on TrS is: 797879.005388998  on VS is: 54061.854566864626  Accuracy: 21.240000000000002 %
E(49) on TrS is: 797869.3890292909  on VS is: 54061.02482142968  Accuracy: 21.26 %
Validation loss is minimum at epoch: 49

As you can see the losses are very high and the learning is very slow.

This is my code:

import numpy as np
from scipy.special import expit
from matplotlib import pyplot as plt
from mnist.loader import MNIST
from sklearn.utils import shuffle


def relu(a, derivative=False):
    f_a = np.maximum(0, a)
    if derivative:
        return (a > 0) * 1
    return f_a  

def softmax(y):
    e_y = np.exp(y - np.max(y, axis=0))
    return e_y / np.sum(e_y, axis=0)

def cross_entropy(y, t, derivative=False, post_process=True):
    epsilon = 10 ** -308
    if post_process:
        if derivative:
            return y - t
        sm = softmax(y)
        sm = np.clip(sm, epsilon, 1 - epsilon)  # avoids log(0)
        return -np.sum(np.sum(np.multiply(t, np.log(sm)), axis=0))

def sigmoid(a, derivative=False):
    f_a = expit(a)
    if derivative:
        return np.multiply(f_a, (1 - f_a))
    return f_a

def identity(a, derivative=False):
    f_a = a
    if derivative:
        return np.ones(np.shape(a))
    return f_a

def accuracy_score(targets, predictions):
    correct_predictions = 0
    for item in range(np.shape(predictions)[1]):
        argmax_idx = np.argmax(predictions[:, item])
        if targets[argmax_idx, item] == 1:
            correct_predictions += 1
    return correct_predictions / np.shape(predictions)[1]


def one_hot(targets):
    return np.asmatrix(np.eye(10)[targets]).T


def plot(epochs, loss_train, loss_val):
    plt.plot(epochs, loss_train)
    plt.plot(epochs, loss_val, color="orange")
    plt.legend(["Training Loss", "Validation Loss"])
    plt.xlabel("Epochs")
    plt.ylabel("Loss")
    plt.grid(True)
    plt.show()

class NeuralNetwork:

    def __init__(self):
        self.layers = []

    def add_layer(self, layer):
        self.layers.append(layer)

    def build(self):
        for i, layer in enumerate(self.layers):
            if i == 0:
                layer.type = "input"
            else:
                layer.type = "output" if i == len(self.layers) - 1 else "hidden"
                layer.configure(self.layers[i - 1].neurons)

    def fit(self, X_train, targets_train, X_val, targets_val, max_epochs=50):
        e_loss_train = []
        e_loss_val = []

        # Getting the minimum loss on validation set
        predictions_val = self.predict(X_val)
        min_loss_val = cross_entropy(predictions_val, targets_val)

        best_net = self  # net which minimize validation loss
        best_epoch = 0  # epoch where the validation loss is minimum

        # batch mode
        for epoch in range(max_epochs):
            predictions_train = self.predict(X_train)
            self.back_prop(targets_train, cross_entropy)
            self.learning_rule(l_rate=0.00001, momentum=0.9)
            loss_train = cross_entropy(predictions_train, targets_train)
            e_loss_train.append(loss_train)

            # Validation
            predictions_val = self.predict(X_val)
            loss_val = cross_entropy(predictions_val, targets_val)
            e_loss_val.append(loss_val)

            print("E(%d) on TrS is:" % epoch, loss_train, " on VS is:", loss_val, " Accuracy:",
                  accuracy_score(targets_val, predictions_val) * 100, "%")

            if loss_val < min_loss_val:
                min_loss_val = loss_val
                best_epoch = epoch
                best_net = self
  
        plot(np.arange(max_epochs), e_loss_train, e_loss_val)

        return best_net

    # Matrix of predictions where the i-th column corresponds to the i-th item
    def predict(self, dataset):
        z = dataset.T
        for layer in self.layers:
            z = layer.forward_prop_step(z)
        return z

    def back_prop(self, target, loss):
        for i, layer in enumerate(self.layers[:0:-1]):
            next_layer = self.layers[-i]
            prev_layer = self.layers[-i - 2]
            layer.back_prop_step(next_layer, prev_layer, target, loss)

    def learning_rule(self, l_rate, momentum):
        # Momentum GD
        for layer in [layer for layer in self.layers if layer.type != "input"]:
            layer.update_weights(l_rate, momentum)
            layer.update_bias(l_rate, momentum)


class Layer:

    def __init__(self, neurons, type=None, activation=None):
        self.dE_dW = None  # derivatives dE/dW where W is the weights matrix
        self.dE_db = None  # derivatives dE/db where b is the bias
        self.dact_a = None  # derivative of the activation function
        self.out = None  # layer output
        self.weights = None  # input weights
        self.bias = None  # layer bias
        self.w_sum = None  # weighted_sum
        self.neurons = neurons  # number of neurons
        self.type = type  # input, hidden or output
        self.activation = activation  # activation function
        self.deltas = None  # for back-prop

    def configure(self, prev_layer_neurons):
        self.set_activation()
        self.weights = np.asmatrix(np.random.normal(-0.1, 0.02, (self.neurons, prev_layer_neurons)))
        self.bias = np.asmatrix(np.random.normal(-0.1, 0.02, self.neurons)).T 


    def set_activation(self):
        if self.activation is None:
            if self.type == "hidden":
                self.activation = sigmoid
            elif self.type == "output":
                self.activation = identity  # will be softmax in cross entropy calculation

    def forward_prop_step(self, z):
        if self.type == "input":
            self.out = z
        else:
            self.w_sum = np.dot(self.weights, z) + self.bias
            self.out = self.activation(self.w_sum)
        return self.out

    def back_prop_step(self, next_layer, prev_layer, target, local_loss):
        if self.type == "output":
            self.dact_a = self.activation(self.w_sum, derivative=True)
            self.deltas = np.multiply(self.dact_a,
                                      local_loss(self.out, target, derivative=True))
        else:
            self.dact_a = self.activation(self.w_sum, derivative=True)  # (m,batch_size)
            self.deltas = np.multiply(self.dact_a, np.dot(next_layer.weights.T, next_layer.deltas))

        self.dE_dW = self.deltas * prev_layer.out.T

        self.dE_db = np.sum(self.deltas, axis=1)

    def update_weights(self, l_rate, momentum):
        # Momentum GD
        self.weights = self.weights - l_rate * self.dE_dW
        self.weights = -l_rate * self.dE_dW + momentum * self.weights

    def update_bias(self, l_rate, momentum):
        # Momentum GD
        self.bias = self.bias - l_rate * self.dE_db
        self.bias = -l_rate * self.dE_db + momentum * self.bias


if __name__ == '__main__':
    mndata = MNIST(path="data", return_type="numpy")
    X_train, targets_train = mndata.load_training()  # 60.000 images, 28*28 features
    X_val, targets_val = mndata.load_testing()  # 10.000 images, 28*28 features

    X_train = X_train / 255  # normalization within [0;1]
    X_val = X_val / 255  # normalization within [0;1]

    X_train, targets_train = shuffle(X_train, targets_train.T)
    X_val, targets_val = shuffle(X_val, targets_val.T)

    # Getting the test set splitting the validation set in two equal parts
    # Validation set size decreases from 10.000 to 5000 (of course)
    X_val, X_test = np.split(X_val, 2)  # 5000 images, 28*28 features
    targets_val, targets_test = np.split(targets_val, 2)
    X_test, targets_test = shuffle(X_test, targets_test.T)

    targets_train = one_hot(targets_train)
    targets_val = one_hot(targets_val)
    targets_test = one_hot(targets_test)

    net = NeuralNetwork()
    d = np.shape(X_train)[1]  # number of features, 28x28
    c = np.shape(targets_train)[0]  # number of classes, 10

    # Shallow network with 1 hidden neuron
    # That is 784, 1, 10
    for m in (d, 1, c):
        layer = Layer(m)
        net.add_layer(layer)

    net.build()

    best_net = net.fit(X_train, targets_train, X_val, targets_val, max_epochs=50)

What I have done:

1. Set 500 instead of 1 hidden neuron
2. Add many hidden layers
3. Decrease/increase learning rate (l_rate) value
4. Decrease/increase momentum (and set it to 0)
5. Replace sigmoid with relu

but there still is the problem.

These are the formulas I used for calculations (but you can check them out from the source code, of course):

Note: f and g in formulas stand for hidden layers activation function and output layer activation function.

EDIT:

I re-implemented the cross_entropy function considering the average loss, replacing

-np.sum(..., axis=0))

with

-np.mean(..., axis=0))

and losses are now comparable. But the problem about low accuracy persists as you can see:

E(0) on TrS is: 2.3033276613180695  on VS is: 2.3021572339654925  Accuracy: 10.96 %
E(1) on TrS is: 2.3021765614184284  on VS is: 2.302430432090161  Accuracy: 10.96 %
E(2) on TrS is: 2.302371681532198  on VS is: 2.302355601340701  Accuracy: 10.96 %
E(3) on TrS is: 2.3023151858432804  on VS is: 2.302364165840666  Accuracy: 10.96 %
E(4) on TrS is: 2.3023186844504564  on VS is: 2.3023457770291267  Accuracy: 10.96 %
...
E(34) on TrS is: 2.2985702635977137  on VS is: 2.2984384616550875  Accuracy: 18.52 %
E(35) on TrS is: 2.2984081462987076  on VS is: 2.2982663840016873  Accuracy: 18.8 %
E(36) on TrS is: 2.2982422912146845  on VS is: 2.298091144330386  Accuracy: 19.06 %
E(37) on TrS is: 2.2980732333918854  on VS is: 2.2979132918897367  Accuracy: 19.36 %
E(38) on TrS is: 2.297901523346666  on VS is: 2.2977333860658424  Accuracy: 19.68 %
E(39) on TrS is: 2.2977277198903883  on VS is: 2.297551989820155  Accuracy: 19.78 %
...
E(141) on TrS is: 2.291884965880953  on VS is: 2.2917100547472575  Accuracy: 21.08 %
E(142) on TrS is: 2.29188099824872  on VS is: 2.291706280301498  Accuracy: 21.08 %
E(143) on TrS is: 2.2918771014203316  on VS is: 2.291702575667588  Accuracy: 21.08 %
E(144) on TrS is: 2.291873271054674  on VS is: 2.2916989365939067  Accuracy: 21.08 %
E(145) on TrS is: 2.2918695030455183  on VS is: 2.291695359057886  Accuracy: 21.08 %
E(146) on TrS is: 2.291865793508291  on VS is: 2.291691839253129  Accuracy: 21.08 %
E(147) on TrS is: 2.2918621387676166  on VS is: 2.2916883735772675  Accuracy: 21.08 %
E(148) on TrS is: 2.2918585353455745  on VS is: 2.291684958620525  Accuracy: 21.08 %
E(149) on TrS is: 2.2918549799506307  on VS is: 2.291681591154936  Accuracy: 21.08 %
E(150) on TrS is: 2.2918514694672263  on VS is: 2.291678268124199  Accuracy: 21.08 %
...
E(199) on TrS is: 2.2916983481535644  on VS is: 2.2915343016441727  Accuracy: 21.060000000000002 %

I incrased MAX_EPOCHS value from 50 to 200 for better visualizing results.

Anecdotic

I think you momentum factor is quite high and constant. Try with a lower or none for verification. – Dahabeah

Maybe you have a mistake in your code? You may try to add another hidden layer to get some information about this idea. If your program returns the same cycles, that will mean you doing something wrong. – Unyoke

This situation called "overfitting" your ANN is training too fast, and it also may be caused by the big rate. Sometimes ANNs trapped in local minimums of the error function, that's why you may get similar situation. – Unyoke

You may write a little bit lower the learning rate. Just relax and enjoy your life ;) – Unyoke

Why using the sigmoid activation function for you problem? Do you have specific information that this activation function performs better than the popular "relu"? (Try relu instead of sigmoid) Also try to add more hidden neurons (5 nodes seems not very much). And my last issue: What is the softmax loss? I only know the cross_entropy loss for softmax activation functions, not the sum between the loss and the output of the activation function. – Titi

Your one-hot encoding method can introduce a bug, when the targets array doesn't contain a sample of the index of the maximum class available (e.g. because your test set doesn't contain a single sample for the digit "9"). Try to crank up your hidden layers (e.g. I used 28, 128, 128, 10; kinda overkill and maybe overfitts, but achieved ACC of 99.8%) and replace the sigmoid by a relu (except for the last layer) – Titi

@MBPictures I edit my network with: 784 (input), 28, 128, 128, 10 (output) neurons with relu on hidden layers and identity on output as you said, but I got 11% accuracy on validation (and losses are horizontal straight lines)... how did you achieve accuracy of 99.8% on my code? – Anecdotic

Oh sorry, I meant 99.8% while using tensorflow. You used identity on output? For output you still need to use softmax as you want to interpret the outputs as probabilities. I'll test your code later on :) but in the meantime you can replace identity by softmax – Titi

I guess you have a bug in your cross_entropy function too. In the inner sum, you pass 2 arguments + axis parameter. But as the second argument already is the positional argument for the axis, I receive an error running your code – Titi

Puh, now I get an RAM overflow exception :D Seems like a memory leak somewhere. Likely because you are trying to fit the model using the whole train set every epoch. Did you try to use some kind of mini batch algorithm instead? – Titi

@Titi Nope, because the "assignment" is about batch learning mode (not mini-batch nor online learning). You can try to reduce the training set size, and check my code on that shrinked set. Anyway I edited my post, please check it out: learning is quite too slow – Anecdotic

Can you share the sources of the formulas you used for softmax, derivations, and categorical cross-entropy loss you used? So we can check that there isn't an issue in the formulas (the values of your losses are a way too high). – Titi

@Titi Yes of course. I have just edited my post with formulas – Anecdotic

@Titi Did you spot any bug? – Anecdotic

Any news?... :| – Convection

There is a movement away from np.matrix (your one hot encoding) for me it's a bit difficult to verify the equations as some need to be elementwise * other the dot product @ . For np.matrix this is quite ambigious – Dahabeah

@Dahabeah Sorry? I haven't understood your comment – Convection

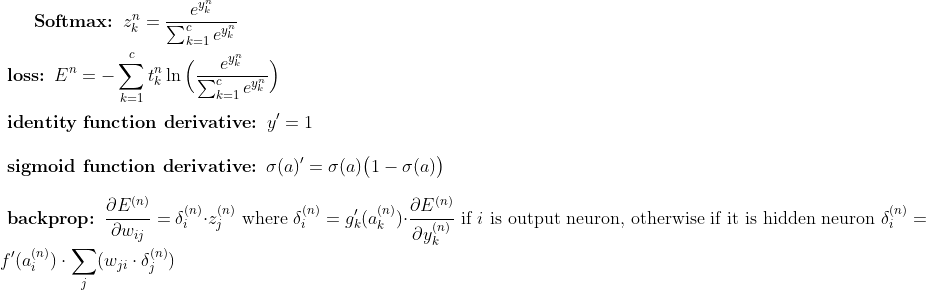
The code mixes ndarrays (e.g X_train) with np.matrixes (e.g. targets_train) these both behave differently when it comes to star * operator. Element wise vs. Dot product. For the latter exits the @ operator. Here it is unclear what data types will the other attributes have.self.deltas is a matrix again, that's not obvious. likewise its not clear if deltas * prev_layer.out.T is an element wise multiplication or a dot product. For a pure ndarray setup it would be obvious a multipication, here it is a dot product. That what makes parts of the code harder to understand. – Dahabeah

@Dahabeah would you suggest to use the same datatype, i.e. ndarrays or matrix? – Convection

@Convection definitely standard numpy arrays. The support of np.matrix for example by scikit-learn is ending. Behind the scenes np.matrix just uses other numpy functions and assures the result is of the same matrix class. What's worst they are not compatible with some numpy functions like argmax(M, axis=-1) – Dahabeah

Answer 1

Combining the changes you and other mentionned, I was able to have it work.

See this gist: https://gist.github.com/theevann/77bb863ef260fe633e3e99f68868f116/revisions

Changes made:

• Use a uniform initialisation (critical)
• Use relu activation (critical)
• Use more hidden layers (critical)
• Comment your SGD momentum as it seems incorrect (not critical)
• Reduce your learning rate (not critical)

I did not look for optimizing it. Obviously using a working momentum GD, using SGD instead of GD, taking the mean to display the loss and tuning the architecture would be logical (if not required) next steps.

Tertiary

This answer is a life-safer. Could you please explain why using an uniform distribution and using ReLU are critical? Could you please explain why my Gradient Descent with Momentum seems to be incorrect? Thank you – Convection

If you want to do GD with Momentum, you should store the previous gradient and do the momentum on the gradient. See for example the formula in: towardsdatascience.com/… – Tertiary

Regarding uniform vs normal, see: datascience.stackexchange.com/questions/13061/…. One is not necessarily better than the other in all cases, but uniform is the default in most DL libraries. One important thing to check is the range / variance of the distribution you use. – Tertiary

Please consider to edit your answer for adding those explanations. – Convection

Answer 2

Two points I observed:

• You are not using mini batches during training. In every step you feed the entire dataset through the network. This is certainly not advisable for anything but simple convex problems. Use mini-batching instead, i.e. chop your dataset into small batches of, say, 32 images and perform update steps per batch, not the entire dataset. Once you have used all batches in the dataset, you have completed one epoch. It depends on the data, the architecture, the optimizer and the learning rate, how many epochs you need.
• You get these huge numbers for training and validation loss because you just sum the losses of all examples and don't divide by the number of samples. You are not computing the average loss per sample, so the two losses are also not comparable.

So my two advices for you are

1. Use mini-batch gradient descent. I am pretty sure this will be a game changer
2. Average the loss per mini-batch, i.e. replace np.sum(np.sum(np.multiply(t, np.log(sm)), axis=0)) with np.mean(np.sum(np.multiply(t, np.log(sm)), axis=0)) to get comparable numbers. I would even also average over classes, so a np.mean(np.multiply(t, np.log(sm))) should do.

Duren

What you mean with "I am pretty sure this will be a game changer"? Will it speed-up convergence and improve accuracy? – Convection

Yes, exactly that – Duren

Answer 3

I'm assuming that the input is 784 nodes, each "connected" to only one pixel. After that there is activation, a hidden dense layer of unknown size (although you mentioned trying 500 nodes), same activation again, 10 nodes and softmax.

1. Firstly it is a bad idea to use sigmoid (vanishing gradients). Try (possibly leaky) relu!

2. Secondly, use the categorical entropy formula for logits instead. That is to say: pass the values without softmaxing them to the loss function (which is of course in a version meant for these values (logits), that is to say you need another formula, easily looked up). When presenting the output it is, however, nice to run it through softmax to get that warm, fuzzy probability feeling. In short, softmax is mainly for human consumption, loss functions needs the extra roughage of the "untreated signal", sort of (actually it's good for efficiency and numerical stability).

3. Thirdly, the categorical cross-entropy is not scale invariant. I don't recommend that you do too much about that (such as try to develop a scale invariant alternative measure), but you could introduce a scale factor to multiply the signal going into the loss function (or if you still use the loss function for the softmaxed signal; going into the softmax function). By twiddling this factor you might be able to get better training efficiency.

4. It is often recommended to use initial weights uniformly (randomly) distributed between ±√(6/(m+n)), where m⨯n is the shape of your weight matrix. Biases are usually initialised to zero.

In bocca al lupo!

Gratifying

I did indeed mean vanishing gradient. I had just used the expression diminishing returns and I got the wires crossed. – Gratifying

According to my knowledge, vanishing gradient problem is related to deep networks; user's project is about a shallow network. – Convection

The gradients are harder to manage in a deep network. I suppose most aspects I've mentioned are more critical for deep networks. Never the less, these are some suggestions that I thought of. I am of course coloured by mainly working with deep networks. – Gratifying