How does Monte Carlo Search Tree work?

Question

Trying to learn MCST using YouTube videos and papers like this one.

http://www0.cs.ucl.ac.uk/staff/D.Silver/web/Applications_files/grand-challenge.pdf

However I am not having much of a luck understanding the details beyond the high level theoretical explanations. Here are some quotes from the paper above and questions I have.

1. Selection Phase: MCTS iteratively selects the highest scoring child node of the current state. If the current state is the root node, where did these children come from in the first place? Wouldn't you have a tree with just a single root node to begin with? With just a single root node, do you get into Expansion and Simulation phase right away?

2. If MCTS selects the highest scoring child node in Selection phase, you never explore other children or possibly even a brand new child whilst going down the levels of the tree?

3. How does the Expansion phase happen for a node? In the diagram above, why did it not choose leaf node but decided to add a sibling to the leaf node?

4. During the Simulation phase, stochastic policy is used to select legal moves for both players until the game terminates. Is this stochastic policy a hard-coded behavior and you are basically rolling a dice in the simulation to choose one of the possible moves taking turns between each player until the end?

5. The way I understand this is you start at a single root node and by repeating the above phases you construct the tree to a certain depth. Then you choose the child with the best score at the second level as your next move. The size of the tree you are willing to construct is basically your hard AI responsiveness requirement right? Since while the tree is being constructed the game will stall and compute this tree.

Commoner

Answer 1

1. Selection Phase: MCTS iteratively selects the highest scoring child node of the current state. If the current state is the root node, where did these children come from in the first place? Wouldn't you have a tree with just a single root node to begin with? With just a single root node, do you get into Expansion and Simulation phase right away?

The selection step is typically implemented not to actually choose among nodes which really exist in the tree (having been created through the Expansion step). It is typically ipmlemented to choose among all possible successor states of the game state matching your current node.

So, at the very beginning, when you have just a root node, you'll want your Selection step to still be able to select one out of all the possible successor game states (even if they don't have matching nodes in the tree yet). Typically you'll want a very high score (infinite, or some very large constant) for game states which have never been visited yet (which don't have nodes in the tree yet). This way, your Selection Step will always randomly select among any states that don't have a matching node yet, and only really use the exploration vs. exploitation trade-off in cases where all possible game states already have a matching node in the tree.

2. If MCTS selects the highest scoring child node in Selection phase, you never explore other children or possibly even a brand new child whilst going down the levels of the tree?

The ''score'' used by the Selection step should typically not just be the average of all outcomes of simulations going through that node. It should typically be a score consisting of two parts; an "exploration" part, which is high for nodes that have been visited relatively infrequently, and an "exploitation" part, which is high for nodes which appear to be good moves so far (where many simulations going through that node ended in a win for the player who's allowed to choose a move to make). This is described in Section 3.4 of the paper you linked. The W(s, a) / N(s, a) is the exploitation part (simply average score), and the B(s, a) is the exploration part.

3. How does the Expansion phase happen for a node? In the diagram above, why did it not choose leaf node but decided to add a sibling to the leaf node?

The Expansion step is typically implemented to simply add a node corresponding to the final game state selected by the Selection Step (following what I answered to your first question, the Selection Step will always end in selecting one game state that has never been selected before).

4. During the Simulation phase, stochastic policy is used to select legal moves for both players until the game terminates. Is this stochastic policy a hard-coded behavior and you are basically rolling a dice in the simulation to choose one of the possible moves taking turns between each player until the end?

The most straightforward (and probably most common) implementation is indeed to play completely at random. It is also possible to do this differently though. You could for example use heuristics to create a bias towards certain actions. Typically, completely random play is faster, allowing you to run more simulations in the same amount of processing time. However, it typically also means every individual simulation is less informative, meaning you actually need to run more simulations for MCTS to play well.

5. The way I understand this is you start at a single root node and by repeating the above phases you construct the tree to a certain depth. Then you choose the child with the best score at the second level as your next move. The size of the tree you are willing to construct is basically your hard AI responsiveness requirement right? Since while the tree is being constructed the game will stall and compute this tree.

MCTS does not uniformly explore all parts of the tree to the same depth. It has a tendency to explore parts which appear to be interesting (strong moves) deeper than parts which appear to be uninteresting (weak moves). So, typically you wouldn't really use a depth limit. Instead, you would use a time limit (for example, keep running iterations until you've spent 1 second, or 5 seconds, or 1 minute, or whatever amount of processing time you allow), or an iteration count limit (for example, allow it to run 10K or 50K or any number of simulations you like).

Artema

What is your reference for this alternative of MCTS? Because what you describe as "typically" is not standard MCTS. – Estoppel

@Estoppel The way I described is is, in my experience, the most common and best way to implement standard (meaning, using UCB1 selection and uniformly random playouts and not all kinds of other bells and whistles) MCTS. I don't typically see people expanding all children/actions at once due to memory concerns, and if you don't, the implementation I described is standard. But there are 100s of different implementations out there, and papers are often lacking in describing these sorts of details. If you think anything is wrong, feel free to post something more clear than some vague insinuations. – Artema

@Estoppel Ok, I see. Imo, talking about "selecting" root is a needless distraction, we simply start there, no need for any selection there. You also forgot to explain the exploration part of typical selection strategies. Apart from that, the only real difference seems to be that you say that Selection is forced to stop after reaching a node that is not fully expanded. The implementation I described is functionally equal (because I suggest assigning infinity to unexpanded actions), but more nicely extends to more advanced MCTSes where we no longer want this (e.g., with trained policy networks) – Artema

Your first paragraph suggests that selection will be made without nodes being present. That doesn't describe the MCTS selection process. Selecting the root node is not a distraction, because the Asker explicitly asks about that. As the expansion phase happens on the selected node (visiting an unvisited child), we need a selected node, and it will be the root in the first iteration of MCTS. – Estoppel

Answer 2

Basically, Monte Carlo is : try randomly many times(*) and then keep the move that led to the best outcome most of the times.

(*) : the number of times and the depth depends on the speed of the decision you want to acheive.

So the root node is always the current game state with immediate children being your possible moves. If you can do 2 moves (yes/no, left/right,...) then you have 2 sub-nodes.

If you cannot do any moves (it may happen depending on the game) then you do not have any decision to make, then Montec Carlo is useless for this move.

If you have X possible moves (chess game) then each possible move is a direct child node.

Then, (in a 2 player game), evey level is alternating "your moves", "opponent moves" and so on.

How to traverse the tree should be random (uniform).

Your move 1 (random move of sub-level 1)

His move 4 (random move of sub-level 2)

Your move 3 (random move of sub-level 3) -> win yay

Pick a reference maximum depth and evaluate how many times you win or lose (or have a sot of evaluation function if the game is not finished after X depth).

You repeat the operation Y times (being quite large) and you select the immediate child node (aka: your move) that leads to you winning most of the times.

This is to evaluate which move you should do now. After this, the opponent moves and it is your turn again. So you have to re-create a tree with the root node being the new current situation and redo the Monte Carlo technique to guess what is your best possible move. And so on.

Romero

Thank you for the general explanation about the MCST but this kind of high level explanations are all available from the resources I linked. What I am after are those specific questions I don't understand now that I am deciding to code up an AI for a game. – Commoner

Answer 3

I was not happy with the currently accepted answer, so I hope this helps some future readers:

If the current state is the root node, where did these children come from in the first place?

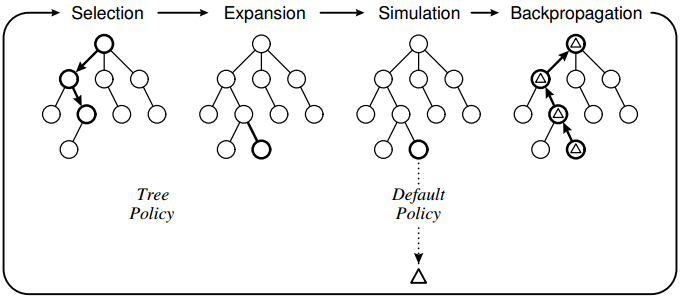
At first there are no children, so the selection phase selects the root node only. The rule is that the selection stops at the node that is not fully expanded, and since the root did not yet expand any child nodes, the root is selected.

Wouldn't you have a tree with just a single root node to begin with? With just a single root node, do you get into Expansion and Simulation phase right away?

Yes.

If MCTS selects the highest scoring child node in Selection phase, you never explore other children or possibly even a brand new child whilst going down the levels of the tree?

Not never, just not in this iteration of the four phases. Scores change after each iteration, so what is considered "best" in one iteration, may not be "best" in the next iteration. However, it is excluded that there would be a non-visited child left aside whilst going down. The selection phase stops when it arrives at a node that has not been fully expanded, i.e. whose children have not all been visited yet. For example, if the root has five children, the first five iterations of the MCTS loop will all select the root node, and then expand into one of those five child nodes -- a different one (randomly) in each iteration (assuming that each iteration makes one expansion), so that after those five iterations the root node is fully expanded.

How does the Expansion phase happen for a node? In the diagram above, why did it not choose leaf node but decided to add a sibling to the leaf node?

The leftmost diagram does not show it, but the selected node in the selection phase knows that there are more children than the one that was already visited, and so the selection phase must stop at that node. Only when in the selection phase we encounter a node that is fully expanded (i.e. where each of the possible children for that node had been visited during an expansion phase), the selection phase continues the traversal downward. Apparently, in the example this was the case for the first two nodes on the selection-path, but not for the third.

During the Simulation phase, stochastic policy is used to select legal moves for both players until the game terminates. Is this stochastic policy a hard-coded behavior and you are basically rolling a dice in the simulation to choose one of the possible moves taking turns between each player until the end?

That's a choice to make. Rolling a dice would be a standard (and fast) method, but you could decide to use some game knowledge, so to exclude the most stupid choices, and give higher probability to potentially good moves. But gathering/calculating such information costs extra time, so it is a trade-off to make. If too much time goes into evaluating moves, the number of nodes that can be visited decreases too much, crippling the power of MCTS.

The way I understand this is you start at a single root node and by repeating the above phases you construct the tree to a certain depth.

The search tree will in general not have its leaves all at the same level. The goal is not to reach a predefined depth. As the selection phase will typically not make random choices, but use an Upper Confidence Bound applied to trees, this could make the tree actually quite unbalanced, as some nodes get selected significantly more often than others.

Then you choose the child with the best score at the second level as your next move.

This is the selection process at any level, but only for as long the node has been fully expanded. Otherwise the not-fully expanded node becomes the selected node.

The size of the tree you are willing to construct is basically your hard AI responsiveness requirement right? Since while the tree is being constructed the game will stall and compute this tree.

That depends how you implement it. The iterations could run in the background, and could be interrupted by some event of your choice: like by reaching a maximum size of the tree, or the time that has elapsed, or a user interaction, ...etc. It could even continue to run while the (human?) opponent thinks about their move. The nice thing is that after each MCTS iteration there is the concept of "best move so far".

Estoppel