I'm having trouble understanding this solution to a problem on HackerRank. Please see the solution code below, apparently by Kimiyuki Onaka.
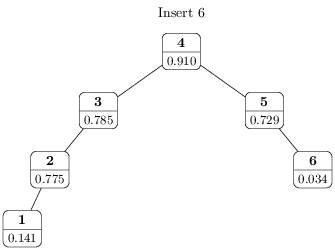
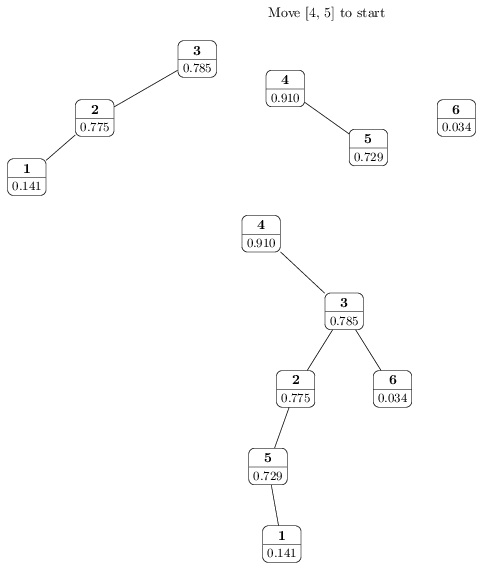
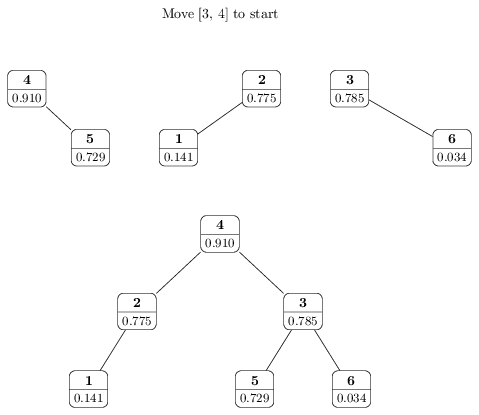
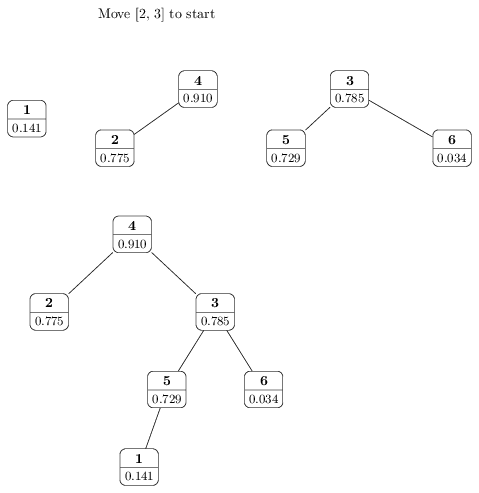
The problem is: given a list of unique numbers, and m queries of the type, "move the current ith to jth elements (l,r) to the beginning", return the final arrangement of the numbers.
Onaka suggests that a treap data structure (one that maintains both priority and binary search) can help solve it in O(m log n). Since I'm not versed in C++, I've tried but failed to conceptualize how a treap could be used. My understanding is that to solve the problem you need log time access to the current ith to jth elements and log time update of the current first element/s and overall order. But I can't see how to conceptualize it.
Ideally, I'd like an explanation in words of how it could be done. Alternatively, just an explanation of what Onaka's code is doing.
Thanks!
#include <iostream>
#include <tuple>
#include <random>
#include <memory>
#define repeat(i,n) for (int i = 0; (i) < (n); ++(i))
using namespace std;
template <typename T>
struct treap {
typedef T value_type;
typedef double key_type;
value_type v;
key_type k;
shared_ptr<treap> l, r;
size_t m_size;
treap(value_type v)
: v(v)
, k(generate())
, l()
, r()
, m_size(1) {
}
static shared_ptr<treap> update(shared_ptr<treap> const & t) {
if (t) {
t->m_size = 1 + size(t->l) + size(t->r);
}
return t;
}
static key_type generate() {
static random_device device;
static default_random_engine engine(device());
static uniform_real_distribution<double> dist;
return dist(engine);
}
static size_t size(shared_ptr<treap> const & t) {
return t ? t->m_size : 0;
}
static shared_ptr<treap> merge(shared_ptr<treap> const & a, shared_ptr<treap> const & b) { // destructive
if (not a) return b;
if (not b) return a;
if (a->k > b->k) {
a->r = merge(a->r, b);
return update(a);
} else {
b->l = merge(a, b->l);
return update(b);
}
}
static pair<shared_ptr<treap>, shared_ptr<treap> > split(shared_ptr<treap> const & t, size_t i) { // [0, i) [i, n), destructive
if (not t) return { shared_ptr<treap>(), shared_ptr<treap>() };
if (i <= size(t->l)) {
shared_ptr<treap> u; tie(u, t->l) = split(t->l, i);
return { u, update(t) };
} else {
shared_ptr<treap> u; tie(t->r, u) = split(t->r, i - size(t->l) - 1);
return { update(t), u };
}
}
static shared_ptr<treap> insert(shared_ptr<treap> const & t, size_t i, value_type v) { // destructive
shared_ptr<treap> l, r; tie(l, r) = split(t, i);
shared_ptr<treap> u = make_shared<treap>(v);
return merge(merge(l, u), r);
}
static pair<shared_ptr<treap>,shared_ptr<treap> > erase(shared_ptr<treap> const & t, size_t i) { // (t \ t_i, t_t), destructive
shared_ptr<treap> l, u, r;
tie(l, r) = split(t, i+1);
tie(l, u) = split(l, i);
return { merge(l, r), u };
}
};
typedef treap<int> T;
int main() {
int n; cin >> n;
shared_ptr<T> t;
repeat (i,n) {
int a; cin >> a;
t = T::insert(t, i, a);
}
int m; cin >> m;
while (m --) {
int l, r; cin >> l >> r;
-- l;
shared_ptr<T> a, b, c;
tie(a, c) = T::split(t, r);
tie(a, b) = T::split(a, l);
t = T::merge(T::merge(b, a), c);
}
repeat (i,n) {
if (i) cout << ' ';
shared_ptr<T> u;
tie(t, u) = T::erase(t, 0);
cout << u->v;
}
cout << endl;
return 0;
}