scipy-optimize-minimize does not perform the optimization - CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL

Question

I am trying to minimize a function defined as follows:

utility(decision) = decision * (risk - cost)

where variables take the following form:

decision = binary array

risk = array of floats

cost = constant

I know the solution will take the form of:

decision = 1 if (risk >= threshold)

decision = 0 otherwise

Therefore, in order to minimize this function I can assume that I transform the function utility to depend only on this threshold. My direct translation to scipy is the following:

def utility(threshold,risk,cost):

     selection_list = [float(risk[i]) >= threshold for i in range(len(risk))]
     v = np.array(risk.astype(float)) - cost

     total_utility = np.dot(v, selection_list)

     return -1.0*total_utility

result = minimize(fun=utility, x0=0.2, args=(r,c),bounds=[(0,1)], options={"disp":True} )

This gives me the following result:

fun: array([-17750.44298655])  hess_inv: <1x1 LbfgsInvHessProduct with
dtype=float64>
jac: array([0.])   
message: b'CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL'
nfev: 2
nit: 0    status: 0   success: True
x: array([0.2])

However, I know the result is wrong because in this case it must be equal to cost. On top of that, no matter what x0 I use, it always returns it as the result. Looking at the results I observe that jacobian=0 and does not compute 1 iteration correctly.

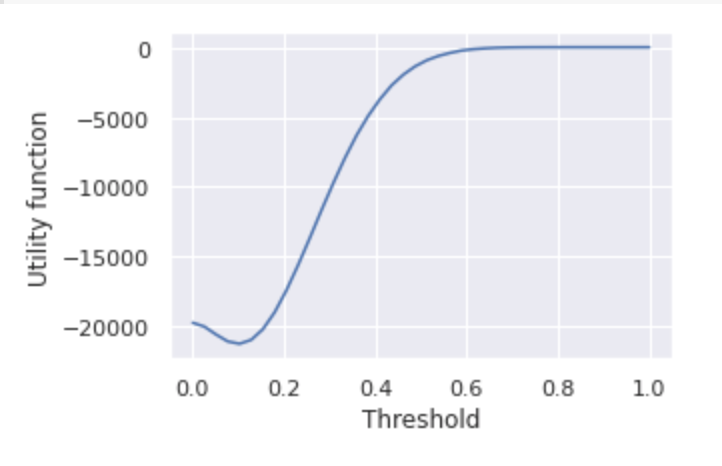
Looking more thoroughly into the function. I plot it and observe that it is not convex on the limits of the bounds but we can clearly see the minimum at 0.1. However, no matter how much I adjust the bounds to be in the convex part only, the result is still the same.

What could I do to minimize this function?

Woodnote

You defined your utility function twice. I assume your question is mostly about the second one, right? – Racecourse

Yes, It's the same thing since we I am saying: utility = decision * (risk - cost) In the code I write: selection_list = decision v = risk - cost utility = dot product{v, selection_list} (which is the multiplication element-wise and sum) Therefore, both expressions are technically the same thing. :) – Woodnote

Answer 1

The error message tells you that the gradient was at some point too small and thus numerically the same as zero. This is likely due to the thresholding that you do when you calculate your selection_list. There you say float(risk[i]) >= threshold, which has derivative 0 almost everywhere. Hence, almost every starting value will give you the warning you receive.

A solution could be to apply some smoothing to the thresholding operation. So instead of float(risk[i]) >= threshold, you would use a continuous function:

def g(x):
    return 1./(1+np.exp(-x))

With this function, you can express the thresholding operation as g((risk[i] - threshold)/a), which a parameter a. The larger a, the closer is this modified error function to what you are doing so far. At something like a=20 or so, you would probably have pretty much the same that you have at the moment. You would therefore derive a sequence of solutions, where you start with a=1 and then take that solution as a starting value for the same problem with a=2, take that solution as a starting value for the problem with a=4, and so on. At some point, you will notice that changing a does no longer change the solution and you're done.

Racecourse