How to do a simple Gaussian mixture sampling and PDF plotting with NumPy/SciPy?

Question

I add three normal distributions to obtain a new distribution as shown below, how can I do sampling according to this distribution in python?

import matplotlib.pyplot as plt
import scipy.stats as ss
import numpy as np


x = np.linspace(0, 10, 1000)
y1 = [ss.norm.pdf(v, loc=5, scale=1) for v in x]
y2 = [ss.norm.pdf(v, loc=1, scale=1.3) for v in x]
y3 = [ss.norm.pdf(v, loc=9, scale=1.3) for v in x]
y = np.sum([y1, y2, y3], axis=0)/3

plt.plot(x, y, '-')
plt.xlabel('$x$')
plt.ylabel('$P(x)$')

BTW, is there a better way to plot such a probability distribution?

Reeve

Are you trying to sample from a Gaussian mixture distribution? – Horwath

Also, please ask one question per post. – Horwath

Yes, could you give me some clue? I think these belong to the same one... @Cong Ma – Reeve

Answer 1

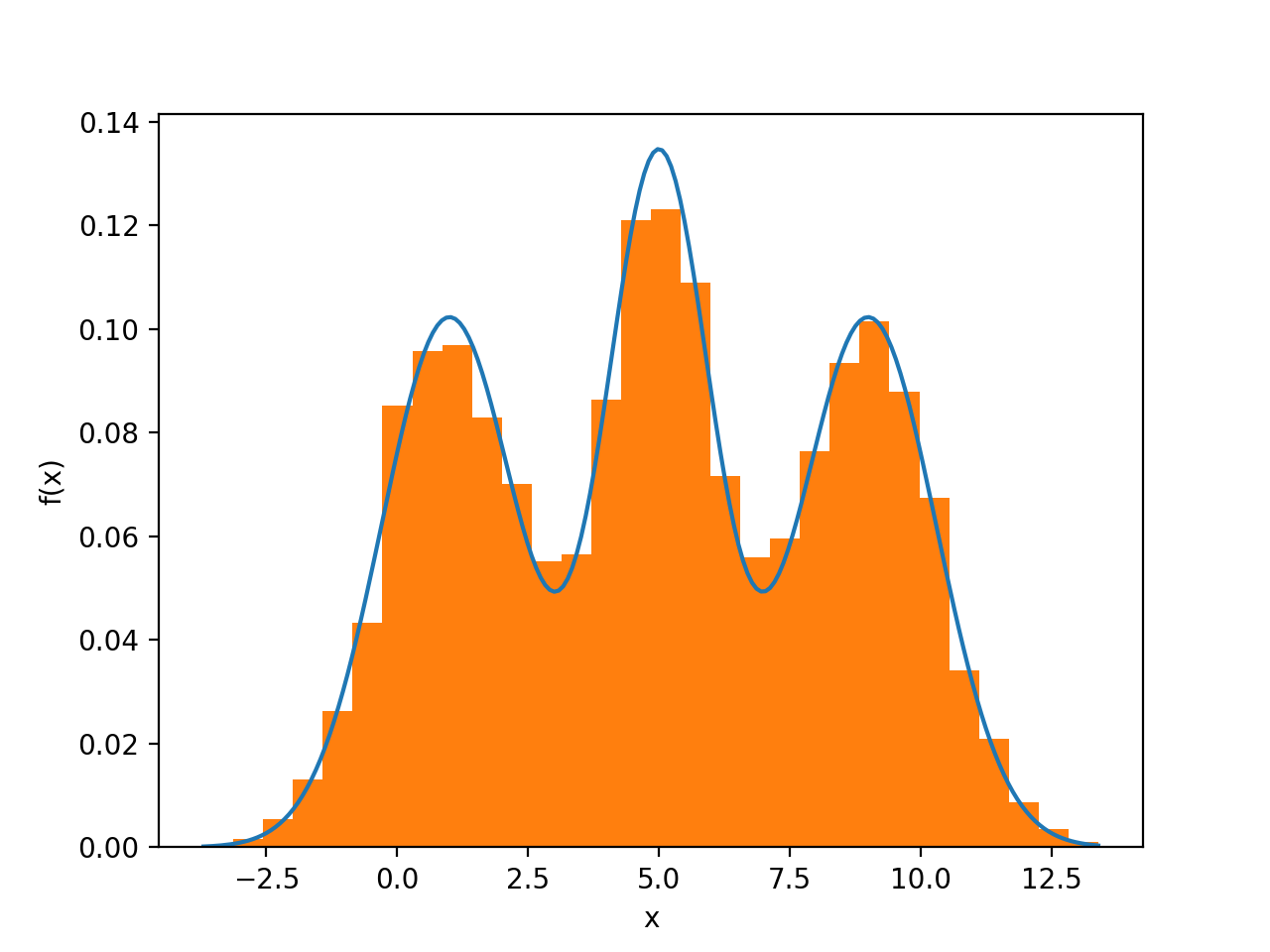
It seems that you're asking two questions: how do I sample from a distribution and how do I plot the PDF?

Assuming you're trying to sample from a mixture distribution of 3 normal ones shown in your code, the following code snipped performs this kind of sampling in the naïve, straightforward way as a proof-of-concept.

Basically, the idea is to

1. Choose an index i among the index of components, i.e. 0, 1, 2 ..., according to their probability weights.
2. Having chosen i, select the corresponding distribution and obtain a sample point from it.
3. Continue from 1 until enough sample points are collected.

However, to plot the PDF, you don't really need a sample in this case, because the theoretical solution is quite easy. In the more general case, the PDF can be approximated by a histogram from the sample.

The code below performs both sampling and PDF-plotting using the theoretical PDF.

import numpy as np
import numpy.random
import scipy.stats as ss
import matplotlib.pyplot as plt

# Set-up.
n = 10000
numpy.random.seed(0x5eed)
# Parameters of the mixture components
norm_params = np.array([[5, 1],
                        [1, 1.3],
                        [9, 1.3]])
n_components = norm_params.shape[0]
# Weight of each component, in this case all of them are 1/3
weights = np.ones(n_components, dtype=np.float64) / 3.0
# A stream of indices from which to choose the component
mixture_idx = numpy.random.choice(len(weights), size=n, replace=True, p=weights)
# y is the mixture sample
y = numpy.fromiter((ss.norm.rvs(*(norm_params[i])) for i in mixture_idx),
                   dtype=np.float64)

# Theoretical PDF plotting -- generate the x and y plotting positions
xs = np.linspace(y.min(), y.max(), 200)
ys = np.zeros_like(xs)

for (l, s), w in zip(norm_params, weights):
    ys += ss.norm.pdf(xs, loc=l, scale=s) * w

plt.plot(xs, ys)
plt.hist(y, normed=True, bins="fd")
plt.xlabel("x")
plt.ylabel("f(x)")
plt.show()

Horwath

Answer 2

In order to make the answer of Cong Ma work more general, I slightly modified his code. The weights work now for any number of mixture components.

import numpy as np
import numpy.random
import scipy.stats as ss
import matplotlib.pyplot as plt

# Set-up.
n = 10000
numpy.random.seed(0x5eed)
# Parameters of the mixture components
norm_params = np.array([[5, 1],
                        [1, 1.3],
                        [9, 1.3]])
n_components = norm_params.shape[0]
# Weight of each component, in this case all of them are 1/3
weights = np.ones(n_components, dtype=np.float64) / float(n_components)
# A stream of indices from which to choose the component
mixture_idx = numpy.random.choice(n_components, size=n, replace=True, p=weights)
# y is the mixture sample
y = numpy.fromiter((ss.norm.rvs(*(norm_params[i])) for i in mixture_idx),
                   dtype=np.float64)

# Theoretical PDF plotting -- generate the x and y plotting positions
xs = np.linspace(y.min(), y.max(), 200)
ys = np.zeros_like(xs)

for (l, s), w in zip(norm_params, weights):
    ys += ss.norm.pdf(xs, loc=l, scale=s) * w

plt.plot(xs, ys)
plt.hist(y, normed=True, bins="fd")
plt.xlabel("x")
plt.ylabel("f(x)")
plt.show()

Fuchsin