How to calculate moving average without keeping the count and data-total?

Question

I am trying to find a way to calculate a moving cumulative average without storing the count and total data that is received so far.

I came up with two algorithms but both need to store the count:

• new average = ((old count * old data) + next data) / next count
• new average = old average + (next data - old average) / next count

The problem with these methods is that the count gets bigger and bigger resulting in losing precision in the resulting average.

The first method uses the old count and next count which are obviously 1 apart. This got me thinking that perhaps there is a way to remove the count but unfortunately I haven't found it yet. It did get me a bit further though, resulting in the second method but still count is present.

Is it possible, or am I just searching for the impossible?

Bladderwort

NB that numerically, storing the current total and current count is the most stable way. Otherwise, for higher counts next/(next count) will start to underflow. So if you are really worried about losing precision, keep the totals! – Mantling

See Wikipedia en.wikipedia.org/wiki/Moving_average – Allyl

Answer 1

You can simply do:

double approxRollingAverage (double avg, double new_sample) {

    avg -= avg / N;
    avg += new_sample / N;

    return avg;
}

Where N is the number of samples where you want to average over. Note that this approximation is equivalent to an exponential moving average. See: Calculate rolling / moving average in C++

Kliber

Don't you have to add 1 to N in this before this line? avg += new_sample / N; – Wheeze

@Wheeze No, because the rolling average is apparently calculated over a fixed number of values (last N values). – Gunmaker

This is not entirely correct. What @Muis describes is an exponentially weighted moving averge, which is sometimes appropriate but is not precisely what the OP requested. As an example, consider the behaviour you expect when most of the points are in the range 2 to 4 but one value is upwards of a million. An EWMA (here) will hold onto traces of that million for quite some time. A finite convolution, as indicated by OP, would lose it immediately after N steps. It does have the advantage of constant storage. – Poleax

That's not a moving average. What you describe is a one pole filter that creates exponential responses to jumps in the signal. A moving average creates a linear response with length N. – Mcdougall

Beware that this is quite far from the common definition of average. If you set N = 5 and enter 5 5 samples, the average will be 0.67. – Bridgeman

I've implemented this algorithm and my running average always increases - it never decreases. obviously that's a concern so I'm not sure what's wrong. – Chao

@DanDascalescu While you're correct that it's not actually a rolling average, your stated value is off by an order of magnitude. With avg initialized to 0, you end up with 3.36 after 5 5s, and 4.46 after 10: cpp.sh/2ryql For long averages, this is certainly a useful approximation. – Orcus

@DanDascalescu this is assuming avg is initialized with 0. If you initialize it to the first element instead, it behaves much better. In your example it will be 5s all the way. – Quartering

Answer 2

New average = old average * (n-1)/n + new value /n

This is assuming the count only changed by one value. In case it is changed by M values then:

new average = old average * (n-len(M))/n + (sum of values in M)/n).

This is the mathematical formula (I believe the most efficient one), believe you can do further code by yourselves

Landre

What is sum of new value? is that different somehow from "new value" in your original formula? – Bille

@Bille in the second example, there are m new values being factored into the new average. I believe that sum of new value here is meant to be the sum of the m new values being used to compute the new average. – Windpollinated

Slightly more efficient for the first one: new_average = (old_average * (n-1) + new_value) / n -- Removes one of the divides. – Instill

How about running average of 3 elements with 6,0,0,9? – Offenbach

When I implement this equation the value or running average always slowly increases. It never goes down - only up. – Chao

Is n the total after adding the new element or before adding the new element? – Catoptrics

@Instill Your solution is perfectly valid but keep in mind that it is much more likely to overflow than the original solution. Depending on the likelihood of overflows over time, one should opt for one approach vs the other. – Louls

@DavidCallanan In this example, after. I agree it is slightly awkward this way. You would have to adjust the formula slightly to use an n that is the total before the new element. – Instill

@Louls Yes, that would be a trade-off. Follow-up questions: Would overflow happen only one iteration sooner? And if these are doubles, would losing precision potentially become a problem well before overflow? – Instill

Answer 3

Here's yet another answer offering commentary on how Muis, Abdullah Al-Ageel and Flip's answer are all mathematically the same thing except written differently.

Sure, we have José Manuel Ramos's analysis explaining how rounding errors affect each slightly differently, but that's implementation dependent and would change based on how each answer were applied to code.

There is however a rather big difference

It's in Muis's N, Flip's k, and Abdullah Al-Ageel's n. Abdullah Al-Ageel doesn't quite explain what n should be, but N and k differ in that N is "the number of samples where you want to average over" while k is the count of values sampled. (Although I have doubts to whether calling N the number of samples is accurate.)

And here we come to the answer below. It's essentially the same old exponential weighted moving average as the others, so if you were looking for an alternative, stop right here.

Exponential weighted moving average

Initially:

average = 0
counter = 0

For each value:

counter += 1
average = average + (value - average) / min(counter, FACTOR)

The difference is the min(counter, FACTOR) part. This is the same as saying min(Flip's k, Muis's N).

FACTOR is a constant that affects how quickly the average "catches up" to the latest trend. Smaller the number the faster. (At 1 it's no longer an average and just becomes the latest value.)

This answer requires the running counter counter. If problematic, the min(counter, FACTOR) can be replaced with just FACTOR, turning it into Muis's answer. The problem with doing this is the moving average is affected by whatever average is initiallized to. If it was initialized to 0, that zero can take a long time to work its way out of the average.

How it ends up looking

Wanting

Well explained. I just miss a plain average in your graph, because that what OP has asked. – Allyl

Maybe I'm missing something, but did you, by chance, mean max(counter, FACTOR). min(counter, FACTOR) will always return FACTOR, right? – Yawp

I believe the point of the min(counter, FACTOR) is to account for the warm up period. Without it, if your FACTOR (or N, or desired sample count) is 1000, then you'll need at least 1000 samples before you get an accurate result, since all updates before that will assume you have 1000 samples, when you may only have 20. – Nomography

It would be nice to stop counting after reaching the factor, probably it would be faster that way. – Shakitashako

The exponentially weighted moving average is really just a terrible Infinite Impulse Response (IIR) low-pass filter. It would likely better to just implement a proper single order Butterworth IIR. I'll need to check again, but I vaguely remember that the gain of the exponentially weighted moving average is not unity, unlike the Butterworth IIR. – Kiehl

Answer 4

From a blog on running sample variance calculations, where the mean is also calculated using Welford's method:

Too bad we can't upload SVG images.

Kiehl

This is similar to what Muis implemented, except that the divide is used a common factor. Thus only one division. – Kiehl

It's actually closer to @Abdullah-Al-Ageel (essentially commutative math) in that Muis doesn't account for incrementing N; copy-paste formula reference: [Avg at n] = [Avg at n-1] + (x - [Avg at n-1]) / n – Trott

@Kiehl & drwaus: Ain't Muis and Abdullah Al-Ageel solutions exactly the same? It's the same computation, just written differently. For me those 3 answers are identital, this one being more visual (too bad we can't use MathJax on SO). – Adley

Answer 5

The answer of Flip is computationally more consistent than the Muis one.

Using double number format, you could see the roundoff problem in the Muis approach:

When you divide and subtract, a roundoff appears in the previous stored value, changing it.

However, the Flip approach preserves the stored value and reduces the number of divisions, hence, reducing the roundoff, and minimizing the error propagated to the stored value. Adding only will bring up roundoffs if there is something to add (when N is big, there is nothing to add)

Those changes are remarkable when you make a mean of big values tend their mean to zero.

I show you the results using a spreadsheet program:

Firstly, the results obtained:

The A and B columns are the n and X_n values, respectively.

The C column is the Flip approach, and the D one is the Muis approach, the result stored in the mean. The E column corresponds with the medium value used in the computation.

A graph showing the mean of even values is the next one:

As you can see, there is big differences between both approachs.

Kickoff

Not really an answer, but useful info. It would be even better if you added 3rd line to your graph, for the true average over n past values, so we could see which of the two approaches comes the closest. – Lucerne

@jpaugh: The B column is alternating between -1.00E+15 and 1.00E+15, so when N is even, the actual mean should be 0. Graph's title is "Even partial means". This means that the 3rd line that you ask about is simply f(x)=0. The graph shows that both approaches introduce errors that keep going up and up. – Brotherton

That's correct, the graph shows exactly the error propagated using big numbers involved in the calculations using both approaches. – Detachment

The legend of your graph has wrong colors: Muis's is orange, Flip's is blue. – Allyl

Answer 6

An example using javascript, for comparison:

https://jsfiddle.net/drzaus/Lxsa4rpz/

function calcNormalAvg(list) {
    // sum(list) / len(list)
    return list.reduce(function(a, b) { return a + b; }) / list.length;
}
function calcRunningAvg(previousAverage, currentNumber, index) {
    // [ avg' * (n-1) + x ] / n
    return ( previousAverage * (index - 1) + currentNumber ) / index;
}

(function(){
  // populate base list
var list = [];
function getSeedNumber() { return Math.random()*100; }
for(var i = 0; i < 50; i++) list.push( getSeedNumber() );

  // our calculation functions, for comparison
function calcNormalAvg(list) {
  	// sum(list) / len(list)
	return list.reduce(function(a, b) { return a + b; }) / list.length;
}
function calcRunningAvg(previousAverage, currentNumber, index) {
  	// [ avg' * (n-1) + x ] / n
	return ( previousAverage * (index - 1) + currentNumber ) / index;
}
  function calcMovingAvg(accumulator, new_value, alpha) {
  	return (alpha * new_value) + (1.0 - alpha) * accumulator;
}

  // start our baseline
var baseAvg = calcNormalAvg(list);
var runningAvg = baseAvg, movingAvg = baseAvg;
console.log('base avg: %d', baseAvg);
  
  var okay = true;
  
  // table of output, cleaner console view
  var results = [];

  // add 10 more numbers to the list and compare calculations
for(var n = list.length, i = 0; i < 10; i++, n++) {
	var newNumber = getSeedNumber();

	runningAvg = calcRunningAvg(runningAvg, newNumber, n+1);
	movingAvg = calcMovingAvg(movingAvg, newNumber, 1/(n+1));

	list.push(newNumber);
	baseAvg = calcNormalAvg(list);

	// assert and inspect
	console.log('added [%d] to list at pos %d, running avg = %d vs. regular avg = %d (%s), vs. moving avg = %d (%s)'
		, newNumber, list.length, runningAvg, baseAvg, runningAvg == baseAvg, movingAvg, movingAvg == baseAvg
	)
results.push( {x: newNumber, n:list.length, regular: baseAvg, running: runningAvg, moving: movingAvg, eqRun: baseAvg == runningAvg, eqMov: baseAvg == movingAvg } );

if(runningAvg != baseAvg) console.warn('Fail!');
okay = okay && (runningAvg == baseAvg);    
}
  
  console.log('Everything matched for running avg? %s', okay);
  if(console.table) console.table(results);
})();

Trott

Answer 7

A neat Python solution based on the above answers:

class RunningAverage():
    def __init__(self):
        self.average = 0
        self.n = 0
        
    def __call__(self, new_value):
        self.n += 1
        self.average = (self.average * (self.n-1) + new_value) / self.n 
        
    def __float__(self):
        return self.average
    
    def __repr__(self):
        return "average: " + str(self.average)

usage:

x = RunningAverage()
x(0)
x(2)
x(4)
print(x)

Amador

Answer 8

In Java8:

LongSummaryStatistics movingAverage = new LongSummaryStatistics();
movingAverage.accept(new data);
...
average = movingAverage.getAverage();

you have also IntSummaryStatistics, DoubleSummaryStatistics ...

Rags

OP is asking for an algorithm, not for a pointer how to compute this in Java. – Mccaslin

Answer 9

( OldAvgValue * OldCount + NewValue * NewCount ) / ( NewCount + OldCount )

Ex : Average Price 20 items is 10 & need to add another 15 items with 10.5 price then, ( 20 * 10 + 15 * 10.5 ) / ( 20 + 15 ) = 10.21

in next cycle if you want to add another 5 with price 11 it would be, ( 35 * 10.21 + 5 * 11 ) / ( 35 + 5 ) = 10.30

Newspaperwoman

Answer 10

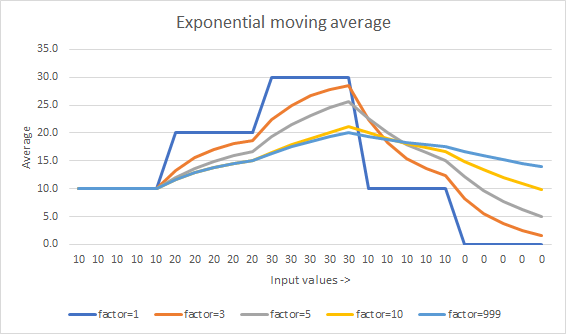
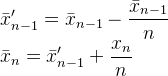Others have mentioned the Welford algorithm. Here is a comparison to Kahan mean algorithm which keeps precision but retains a sum (see demo).

package main

import (
    "fmt"
    "os"
)

func main() {
    values := []float64{
        1,
        2.1,
        3.12,
        4.123,
        5.1234,
        6.1234567890123456789,
        7.12345678901234567890123,
    }

    fmt.Printf("\nKahan mean . . .\n\n")
    compareClassicAndKahan(values)

    fmt.Printf("\nWelford mean . . .\n\n")
    compareClassicAndWelford(values)
}

func compareClassicAndKahan(values []float64) {
    sum := float64(0)
    runningMean := float64(0)
    kahanSum := float64(0)
    compensation := float64(0)

    for i := 0; i < len(values); i++ {
        x := values[i]
        count := float64(i + 1)

        // Classic mean
        sum += x
        classicMean := sum / count

        // Kahan mean
        y := x - compensation
        t := kahanSum + y
        compensation = (t - kahanSum) - y
        kahanSum = t
        runningMean = kahanSum / count

        checkResult("kahan", count, classicMean, runningMean)
    }
}

func compareClassicAndWelford(values []float64) {
    sum := float64(0)
    runningMean := float64(0)

    for i := 0; i < len(values); i++ {
        x := values[i]
        count := float64(i + 1)

        // Classic mean
        sum += x
        classicMean := sum / count

        // Welford mean
        runningMean += (x - runningMean) / count

        // Print Results
        checkResult("welford", count, classicMean, runningMean)
    }
}

func checkResult(
    name string,
    count, classicMean, runningMean float64,
) {
    s := fmt.Sprintf(
        "%s %f classicMean=%64.64f\n"+
            "%s %f runningMean=%64.64f\n\n",
        name,
        count,
        classicMean,
        name,
        count,
        runningMean,
    )
    if classicMean == runningMean {
        fmt.Printf(s)
    } else {
        fmt.Fprint(os.Stderr, s)
    }
}

Kahan means match the classic summation method:

kahan 1.000000 classicMean=1.0000000000000000000000000000000000000000000000000000000000000000
kahan 1.000000 runningMean=1.0000000000000000000000000000000000000000000000000000000000000000

kahan 2.000000 classicMean=1.5500000000000000444089209850062616169452667236328125000000000000
kahan 2.000000 runningMean=1.5500000000000000444089209850062616169452667236328125000000000000

kahan 3.000000 classicMean=2.0733333333333336945258906780509278178215026855468750000000000000
kahan 3.000000 runningMean=2.0733333333333336945258906780509278178215026855468750000000000000

kahan 4.000000 classicMean=2.5857499999999999928945726423989981412887573242187500000000000000
kahan 4.000000 runningMean=2.5857499999999999928945726423989981412887573242187500000000000000

kahan 5.000000 classicMean=3.0932800000000000295585778076201677322387695312500000000000000000
kahan 5.000000 runningMean=3.0932800000000000295585778076201677322387695312500000000000000000

kahan 6.000000 classicMean=3.5983094648353906030990856379503384232521057128906250000000000000
kahan 6.000000 runningMean=3.5983094648353906030990856379503384232521057128906250000000000000

kahan 7.000000 classicMean=4.1019019397178126951075682882219552993774414062500000000000000000
kahan 7.000000 runningMean=4.1019019397178126951075682882219552993774414062500000000000000000

Welford mean has some matches, sortof fixes itself:

welford 1.000000 classicMean=1.0000000000000000000000000000000000000000000000000000000000000000
welford 1.000000 runningMean=1.0000000000000000000000000000000000000000000000000000000000000000

welford 2.000000 classicMean=1.5500000000000000444089209850062616169452667236328125000000000000
welford 2.000000 runningMean=1.5500000000000000444089209850062616169452667236328125000000000000

// welford 3.000000 error see below

welford 4.000000 classicMean=2.5857499999999999928945726423989981412887573242187500000000000000
welford 4.000000 runningMean=2.5857499999999999928945726423989981412887573242187500000000000000

welford 5.000000 classicMean=3.0932800000000000295585778076201677322387695312500000000000000000
welford 5.000000 runningMean=3.0932800000000000295585778076201677322387695312500000000000000000

// welford 6.000000 error see below

welford 7.000000 classicMean=4.1019019397178126951075682882219552993774414062500000000000000000
welford 7.000000 runningMean=4.1019019397178126951075682882219552993774414062500000000000000000

Welford mismatches (errors):

welford 3.000000 classicMean=2.0733333333333336945258906780509278178215026855468750000000000000
welford 3.000000 runningMean=2.0733333333333332504366808279883116483688354492187500000000000000

welford 6.000000 classicMean=3.5983094648353906030990856379503384232521057128906250000000000000
welford 6.000000 runningMean=3.5983094648353910471882954880129545927047729492187500000000000000

Holofernes