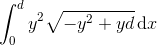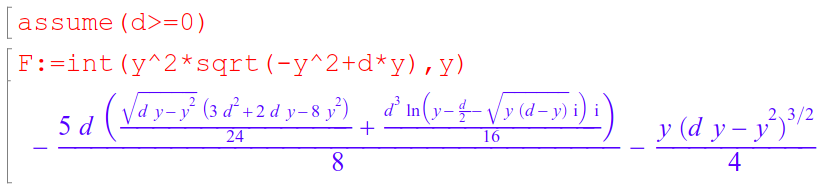Why does MATLAB give a negative value for this integration?

Question

I'm trying do the following integration:

where d >= 0.

I try to get an explicit expression and I think the result should be a positive value since the integrand is greater or equal to 0, but the symbolic integration of MATLAB gave me this result:

syms y d
assume(d>=0)
int(y^2*sqrt(-y^2+d*y),y,0,d)

ans =

-(5*pi*d^4)/128

So I am wondering why a negative value appeared. Do you know how to interpret this result?

Taeniafuge

I find this absolutely fascinating and would like to know the answer, but I guess the question is better asked in stackoverflow under the matlab tag. Perhaps one of the moderators can transfer it there? – Canonry

FWIW, Maple gives $+5d^4\pi/128$, so it seems that it is just the sign that is wrong. But this seems to be a pure software issue and nothing really to do with mathematics, so I will vote to close the question here. – Reductase

Mathematica gives the correct answer. – Reclinate

Thanks for your help, – Taeniafuge

Maybe this is one for mathoverflow.net/questions/11517/computer-algebra-errors ? – Pharaoh

(Oops, sorry, I got here from MO and didn't notice it had migrated.) – Pharaoh

Yes, clearly a bug. Tricky!..... mathoverflow.net/questions/11517/computer-algebra-errors/… – Embark

Answer 1

This is very clearly a bug, and I've already submitted a bug report with The MathWorks. You can confirm it by plotting the integrand and noting it is always positive over the range [0 d], thus assuring that the integral should yield a positive value:

h = [];
for d = 1:5,
  y = linspace(0, d, 1000);
  h = [h; plot(y, f(y, d))];
  hold on;
end
legend(h, strcat({'d = '}, int2str((1:5).')));
xlabel('y');
ylabel('f(y)');
title('f(y) = y^2*sqrt(d*y - y^2)');

Update #1:

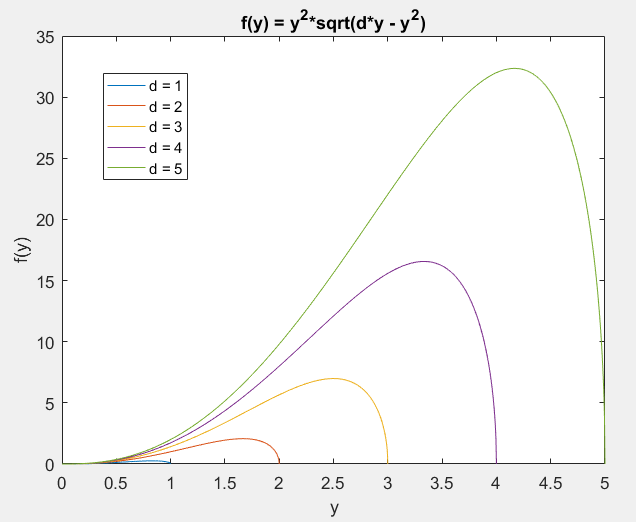
A response from The MathWorks suggest that this may be an issue with the MuPad command limit. Below is the indefinite integral found in MuPad:

Evaluating this at y=d gives the correct result, but evaluating it in the limit as y approaches 0 gives different results based on whether d is substituted before or after the limit calculation. Here's an example with d=1:

Note the change in sign of the first term. In this case, substituting for d before the limit calculation results in a positive (and correct) evaluation of the integral. MATLAB therefore appears to be substituting for d after the limit calculation, giving the erroneous negative result for the definite integral.

Update #2:

I received a follow-up response stating that this bug has now been addressed in the latest release, R2018b. I was able to confirm in the R2018b pre-release that the two limit calculations above produce the same result, and that the integration result now has the proper sign:

syms y d
assume(d >= 0)
int(y^2*sqrt(-y^2+d*y), y, 0, d)

ans =

(5*pi*d^4)/128

Justus