How to display a 3D plot of a 3D array isosurface with mplot3D or similar

Question

I have a 3-dimensional numpy array. I'd like to display (in matplotlib) a nice 3D plot of an isosurface of this array (or more strictly, display an isosurface of the 3D scalar field defined by interpolating between the sample points).

matplotlib's mplot3D part provides nice 3D plot support, but (so far as I can see) its API doesn't have anything which will simply take a 3D array of scalar values and display an isosurface. However, it does support displaying a collection of polygons, so presumably I could implement the marching cubes algorithm to generate such polygons.

It does seem quite likely that a scipy-friendly marching cubes has already been implemented somewhere and that I haven't found it, or that I'm missing some easy way of doing this. Alternatively I'd welcome any pointers to other tools for visualising 3D array data easily usable from the Python/numpy/scipy world.

Remiss

Matplotlib's 3D plotting really isn't intended for things like this. (It's meant to produce vector output for simple 3D plots, not be a full 3D plotting engine.) Use mayavi/mlab if you want isosurfaces. – Engineer

Answer 1

Just to elaborate on my comment above, matplotlib's 3D plotting really isn't intended for something as complex as isosurfaces. It's meant to produce nice, publication-quality vector output for really simple 3D plots. It can't handle complex 3D polygons, so even if implemented marching cubes yourself to create the isosurface, it wouldn't render it properly.

However, what you can do instead is use mayavi (it's mlab API is a bit more convenient than directly using mayavi), which uses VTK to process and visualize multi-dimensional data.

As a quick example (modified from one of the mayavi gallery examples):

import numpy as np
from enthought.mayavi import mlab

x, y, z = np.ogrid[-10:10:20j, -10:10:20j, -10:10:20j]
s = np.sin(x*y*z)/(x*y*z)

src = mlab.pipeline.scalar_field(s)
mlab.pipeline.iso_surface(src, contours=[s.min()+0.1*s.ptp(), ], opacity=0.3)
mlab.pipeline.iso_surface(src, contours=[s.max()-0.1*s.ptp(), ],)

mlab.show()

Engineer

Perfect! apt-get install mayavi2, ran your code... Just Works. Exactly what I'm looking for. I'd been wondering for years whether I shouldn't make use of VTK somehow; this looks like a nice way into it from the scipy world. OMG it's like discovering a whole new planet... – Remiss

And there's an mlab contour3d function to make stuff like the above even simpler: github.enthought.com/mayavi/mayavi/auto/… – Remiss

Just to warn you, the "list of specific values to contour" functionality in contour3d has been broken for quite awhile. (It may have been fixed recently, but don't be surprised if it doesn't work.) It sill works perfectly if you just want, say, 5 contours between the min and max, but passing in a list of specific values (e.g. [0.1, 0.5, 0.9, 1.5, 2.5]) will silently fail. By and large, though, it's quite slick and that's the only annoying bug I've run into! It handles very large datasets very well, too! – Engineer

Cancel that, passing in a list of specific values seems to work perfectly in the latest version, for whatever it's worth. – Engineer

I've just been looking at it working well with some 512^3 arrays. Interestingly, contour3d's peak memory consumption seems considerably lower than the "pipeline" version above (about 2.5GB vs 8GB; fortunately I'm on a big 64 bit system). Haven't tried doing anything with things like np.array(...,dtype=np.int16) yet though (I think np arrays default to double). – Remiss

on ubuntu 15.04, I add to modify your a little bit as follow: from mayavi import mlab – Zebulun

Can you obtain the .obj file from the data? and if yes, how? – Morrison

If only mayavi would work "out of the box" both standalone and in jupyter as matplotlib does... It's a huge pita to get it setup, sadly :-( – Caughey

Answer 2

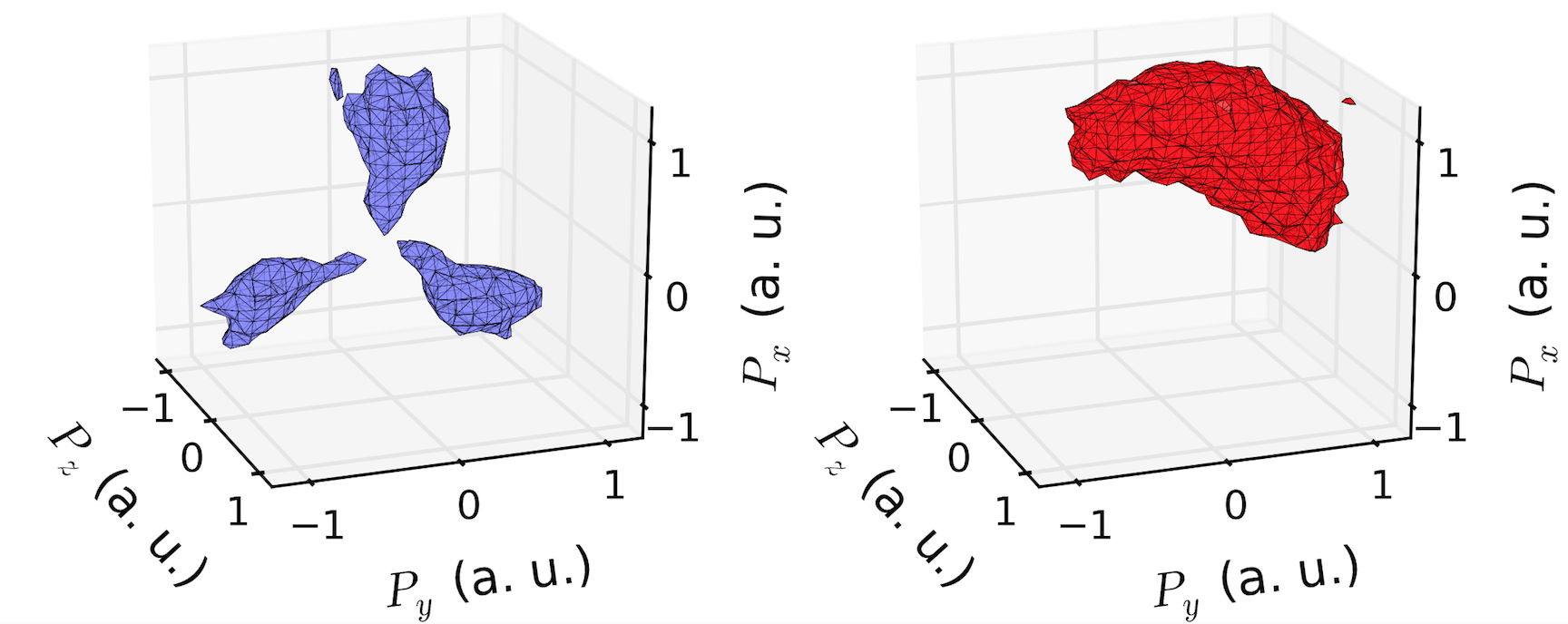
Complementing the answer of @DanHickstein, you can also use trisurf to visualize the polygons obtained in the marching cubes phase.

import numpy as np
from numpy import sin, cos, pi
from skimage import measure
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
   
   
def fun(x, y, z):
    return cos(x) + cos(y) + cos(z)
    
x, y, z = pi*np.mgrid[-1:1:31j, -1:1:31j, -1:1:31j]
vol = fun(x, y, z)
iso_val=0.0
verts, faces = measure.marching_cubes(vol, iso_val, spacing=(0.1, 0.1, 0.1))

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_trisurf(verts[:, 0], verts[:,1], faces, verts[:, 2],
                cmap='Spectral', lw=1)
plt.show()

Update: May 11, 2018

As mentioned by @DrBwts, now marching_cubes return 4 values. The following code works.

import numpy as np
from numpy import sin, cos, pi
from skimage import measure
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D


def fun(x, y, z):
    return cos(x) + cos(y) + cos(z)

x, y, z = pi*np.mgrid[-1:1:31j, -1:1:31j, -1:1:31j]
vol = fun(x, y, z)
iso_val=0.0
verts, faces, _, _ = measure.marching_cubes(vol, iso_val, spacing=(0.1, 0.1, 0.1))

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_trisurf(verts[:, 0], verts[:,1], faces, verts[:, 2],
                cmap='Spectral', lw=1)
plt.show()

Update: February 2, 2020

Adding to my previous answer, I should mention that since then PyVista has been released, and it makes this kind of tasks somewhat effortless.

Following the same example as before.

from numpy import cos, pi, mgrid
import pyvista as pv

#%% Data
x, y, z = pi*mgrid[-1:1:31j, -1:1:31j, -1:1:31j]
vol = cos(x) + cos(y) + cos(z)
grid = pv.StructuredGrid(x, y, z)
grid["vol"] = vol.flatten()
contours = grid.contour([0])

#%% Visualization
pv.set_plot_theme('document')
p = pv.Plotter()
p.add_mesh(contours, scalars=contours.points[:, 2], show_scalar_bar=False)
p.show()

With the following result

Update: February 24, 2020

As mentioned by @HenriMenke, marching_cubes has been renamed to marching_cubes_lewiner. The "new" snippet is the following.

import numpy as np
from numpy import cos, pi
from skimage.measure import marching_cubes_lewiner
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

x, y, z = pi*np.mgrid[-1:1:31j, -1:1:31j, -1:1:31j]
vol = cos(x) + cos(y) + cos(z)
iso_val=0.0
verts, faces, _, _ = marching_cubes_lewiner(vol, iso_val, spacing=(0.1, 0.1, 0.1))

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_trisurf(verts[:, 0], verts[:,1], faces, verts[:, 2], cmap='Spectral',
                lw=1)
plt.show()

Fantastically

marching_cubes now returns 4 values the above code works if you change to verts, faces, sumit, sumitelse = measure.marching_cubes(vol, 0, spacing=(0.1, 0.1, 0.1)) – Alec

@AndrasDeak, I would say that the documentation is really good and with lots of examples. That being said, it is a bit different to use but not too difficult. – Fantastically

OK, I've given the PyVista docs a closer inspection. You're right, it seems really flexible and powerful, even if its API seems a bit different from what I'm used to, and the docs really are full of examples and helpful cross-links. I'll definitely give it a go sometime. – Goggler

Seems like marching_cubes has been renamed to marching_cubes_lewiner. – Fortyish

The only problem with trisurf is the colormap : it will follow the Z axis (verts[:,2]), it doesn't have facecolors with can be problematic for quantitative evaluation Even though mayavi is said to be complicated, it can plot iso_surface but you can also export the data into XML and deal with Paraview or other VTK viewer – Exude

Answer 3

If you want to keep your plots in matplotlib (much easier to produce publication-quality images than mayavi in my opinion), then you can use the marching_cubes function implemented in skimage and then plot the results in matplotlib using

mpl_toolkits.mplot3d.art3d.Poly3DCollection

as shown in the link above. Matplotlib does a pretty good job of rendering the isosurface. Here is an example that I made of some real tomography data:

Thrilling

Answer 4

Since the initial post was submitted, enhancements and additional packages for Matplotlib have become available. This has made Matplotlib a viable method for creating many types of 'complex' 3D plots.

Two major advantages of using Matplotlib are the ease of showing coordinate axes and using multiple axes (subplots) in the same figure. Using these two abiliies can enhance a concept. For example, the periodic nature of the isometric surface is 'shown' in the following figure:

This 3D figure shows that the 'negative' space is pi shifted from the 'positive' space by using different colors for the front and back surface. This figure was generated using S3Dlib, a Matplotlib 3rd party package, along with scikit-image. The heavy lifting of rendering is done by Matplotlib. The code is:

import numpy as np
from skimage.measure import marching_cubes_lewiner
import matplotlib.pyplot as plt
import s3dlib.surface as s3d
import s3dlib.cmap_utilities as cmu

bcmap = cmu.binary_cmap('orange', 'yellowgreen')
# ...................................................................
fig = plt.figure(figsize=plt.figaspect(.5))
minmax = (-2*np.pi, 2*np.pi)
for i,[dmn,title] in enumerate ( [ \
        [2*np.pi, r'-2$\pi$ < surface < 2$\pi$'],
        [  np.pi,  r'-$\pi$ < central section < $\pi$']   ] ) :
    
    x, y, z = dmn*np.mgrid[-1:1:61j, -1:1:61j, -1:1:61j]
    vol = np.cos(x) + np.cos(y) + np.cos(z)  # Schwarz P 
    verts, faces, _, _ = marching_cubes_lewiner(vol, 0.001, (0.1, 0.1, 0.1))
    verts = dmn*( verts-(3,3,3) )/3
    surface = s3d.Surface3DCollection( verts, faces, cmap=bcmap)
    
    ax =fig.add_subplot(121+i, projection='3d')
    ax.set(xlabel='X',ylabel='Y',zlabel='Z',title=title,
        xlim=minmax,ylim=minmax,zlim=minmax )
    surface.map_cmap_from_normals(direction=ax)
    ax.add_collection3d(surface.shade(.3).hilite(0.7,focus=2))

fig.tight_layout()
plt.show()

The use of subplots also provides a demonstration of functional parameters on 3D surface geometry. For example, order and degree in spherical harmonics are visualized using a table of surfaces in the following figure:

The code to generate this figure is given at spherical harmonic example and uses the SciPy package for the spherical harmonics function.

Proof

Currently 8 out of your 10 answers uses and links to s3dlib in an unsolicited way, and there's no clear indication that you are the author of that package. I recommend adding disclaimers about your authorship to your answers/profile, see e.g. "how not to be a spammer?" in the Help Center and this meta post. Other than the affiliation disclosure you're probably fine. – Goggler