What are the mathematical/computational principles behind this game?

Question

My kids have this fun game called Spot It! The game constraints (as best I can describe) are:

• It is a deck of 55 cards
• On each card are 8 unique pictures (i.e. a card can't have 2 of the same picture)
• Given any 2 cards chosen from the deck, there is 1 and only 1 matching picture.
• Matching pictures may be scaled differently on different cards but that is only to make the game harder (i.e. a small tree still matches a larger tree)

The principle of the game is: flip over 2 cards and whoever first picks the matching picture gets a point.

Here's a picture for clarification:

(Example: you can see from the bottom 2 cards above that the matching picture is the green dinosaur. Between the bottom-right and middle-right picture, it's a clown's head.)

I'm trying to understand the following:

1. What are the minimum number of different pictures required to meet these criteria and how would you determine this?

2. Using pseudocode (or Ruby), how would you generate 55 game cards from an array of N pictures (where N is the minimum number from question 1)?

Update:

Pictures do occur more than twice per deck (contrary to what some have surmised). See this picture of 3 cards, each with a lightning bolt:

Utricle

Minimum number of pictures per card, or minimum number of pictures given that there are 8 per card? Also, does every picture have to be matchable? – Raveaux

I think you need to add more constraints. Otherwise, you could put an apple on every card, and then add any number of unique images to each card. Each pair of cards will only match on the image of the apple. – Marijo

@Marijo I guess every picture only occurs twice per deck. – Robena

@mbeckish: If you did that then you wouldn't get the minimum number of pictures required. – Rawalpindi

Excellent puzzle! Probably connected with (Finite) Projective Geometries. – Archerfish

@WTP - If that were the case, then You could have at most K cards in the deck, where K is the number of pictures on each card. If you want to have more cards in your deck, you would need to allow the same image to be involved in matching multiple pairs of cards. – Marijo

Ok, I've updated the original question to try and clarify the comments here. @WTP pictures occurs much more often than twice per deck. – Utricle

@WTP and int the picture he posted there are 3 cards sharing same picture (spot them!) – Playground

@Callmeed: If there were 57 (and not 55) cards in your set, I would bet that all pictures appear in exactly 8 cards. Now, I can bet that almost all pictures appear in 8 cards, except 14 pictures that appear in 7 cards and 1 picture that appears in 6 cards. – Archerfish

Oh, and there is a total of exactly 57 different pictures in the set. – Archerfish

@cabaret: In that case you'll like set. Unbelievably fun and aggravating. – Baillieu

Great looking game. Going to have to pick that up for my kids. – Succentor

This should probably be on Mathematics – Toneless

Am I allowed to cross-post this on Math SE? – Utricle

@Calmeed: I guess you can probably cross-post it, but keep the objectives separate. If you post there, ask for the deeper mathematical details behind the game (no programming) and leave the Ruby/programming details for SO. – Gorman

Ok, there's already a post about this game on Math. See math.stackexchange.com/questions/36798/…. According to a link on that post, there are 50 different pictures. No accepted answer though. – Utricle

@Callmeed: i posted a link to your question there, perhaps someone is also interested in this discussion here. – Hayrack

While this is a great question, its already been asked on the math site (by me). It seems a little off topic here. - math.stackexchange.com/questions/36798/… – Millepede

This is a very interesting question with very interesting answers but it's also very off-topic for SO. :( – Sidestroke

About the mathematical principles, see also David Madore's recent writeup "Le jeu de cartes Dobble et la géométrie projective expliquée aux enfants" madore.org/~david/weblog/… (note that "Dobble" is another for this game). See also math.stackexchange.com/q/464932/24908 , math.stackexchange.com/q/172771/24908 , math.stackexchange.com/q/36798/24908 – Poser

Out of the topic : I found similar game on android play store play.google.com/store/apps/details?id=com.game.findone – Chopfallen

For working JS code, see https://mcmap.net/q/129295/-spot-it-algorithm-js/87520 – Bassesalpes

Answer 1

Finite Projective Geometries

The axioms of projective (plane) geometry are slightly different than the Euclidean geometry:

• Every two points have exactly one line that passes through them (this is the same).
• Every two lines meet in exactly one point (this is a bit different from Euclid).

Now, add "finite" into the soup and you have the question:

Can we have a geometry with just 2 points? With 3 points? With 4? With 7?

There are still open questions regarding this problem but we do know this:

• If there are geometries with Q points, then Q = n^2 + n + 1 and n is called the order of the geometry.

• There are n+1 points in every line.

• From every point, pass exactly n+1 lines.

• Total number of lines is also Q.

• And finally, if n is prime or a prime power, then there does exists a geometry of order n.

---

What does that have to do with the puzzle, one may ask.

Put card instead of point and picture instead of line and the axioms become:

• Every two cards have exactly one picture in common.
• For every two pictures there is exactly one card that has both of them.

Now, lets take n=7 and we have the order-7 finite geometry with Q = 7^2 + 7 + 1 . That makes Q=57 lines (pictures) and Q=57 points (cards). I guess the puzzle makers decided that 55 is more round number than 57 and left 2 cards out.

We also get n+1 = 8, so from every point (card), 8 lines pass (8 pictures appear) and every line (picture) has 8 points (appears in 8 cards).

---

Here's a representation of the most famous finite projective (order-2) plane (geometry) with 7 points, known as Fano Plane, copied from Noelle Evans - Finite Geometry Problem Page

I was thinking of creating an image that explain how the above order-2 plane could be made a similar puzzle with 7 cards and 7 pictures, but then a link from the math.exchange twin question has exactly such a diagram: Dobble-et-la-geometrie-finie

Koodoo

So this game exhibits non-Euclidean geometry? Would it be correct to say that The Cards Are Right? – Salt

This sounds awesome, but I have no certainty that it actually models the problem well. @ypercube, could you explain a bit more why you think the analogy between card/picture and point/line is valid? – Radiopaque

@Nate: The 1st analogy every two cards have exactly one picture in common, is stated in the question. The 2nd for every two pictures there is exactly one card that has both of them, the OP can tell us if the game set satisfies it. – Archerfish

Awesome answer! Great insight, realizing that the game matches the properties of an Order-7 Projective Plane, plus one of the best explanations of Projective Planes for laypersons that I have seen. – Wollastonite

@ypercube +1 Brilliant :D This is just more than an answer to a question. – Tound

Brilliant. I'm going to need to read this 100 more times to try to figure out how to generate card sets in Python... – Influential

Does this mean, that you can't solve the problem for non prime n? Or is it just not represented by the projective plane approach? – Glazunov

@Glazunov actually, solution exists for prime and prime powers (4,8,19,16,25,27,32,...). For the other composite numbers, it's mostly an open problem. I think I should update the answer with more details. – Archerfish

Answer 2

For those who have trouble picturing the projective plane geometry with 57 points, there is a really nice, intuitive way to construct the game with 57 cards and 57 symbols (based on the answer by Yuval Filmus for this question):

1. For cards with 8 symbols, create a 7x7 grid of unique symbols.
2. Add an additional 8 symbols for the "slopes" from 0 to 6, plus one for infinity slope.
3. Each card is a line on the grid (7 symbols) plus one symbol from the slope set for the slope of the line. Lines have an offset (i.e. starting point on the left), and a slope (i.e. how many symbols to go up for each step right). When the line leaves the grid at the top, re-enter at the bottom. See this example figure (pictures from boardgamegeek) for two such cards:

In the example, I take one line with slope zero (red), and one with slope 1 (green). They intersect at exactly one common point (the owl).

This method ensures that any two cards have exactly one common symbol, because

1. If the slopes are different, then the lines will always intersect at exactly one point.
2. If the slopes are the same, then the lines will not intersect and there will be no common symbol from the grid. In this case, the slope symbol will be the same.

In this way, we can construct 7x7 cards (7 offsets and 7 slopes).

We can also construct seven additional cards from vertical lines through the grid (i.e. taking each column). For those, the infinity slope icon is used.

Because each card consists of seven symbols from the grid and exactly one "slope" symbol, we can create one additional card, which simply consists of all the 8 slope symbols.

This leaves us with 7x8 + 1 = 57 possible cards, and 7 x 7 + 8 = 57 required symbols.

(Naturally, this only works with a prime-number-sized grid (e.g. n=7). Otherwise, lines of different slope could have zero or more than one intersection if the slope is a divisor of the grid size.)

Jipijapa

Does this mean that the is no solution for n being no prime or only that this method does not work then? – Glazunov

@Glazunov This particular method would not work. Other methods may still exist. A simple method that has been posted here (and that "works" with any number of symbols) would be to just brute force random cards until you have a deck. – Jipijapa

What a clear answer - thank you for making the graphics! I have implemented it in JS at https://mcmap.net/q/129295/-spot-it-algorithm-js – Bassesalpes

Answer 3

So there are k=55 cards containing m=8 pictures each from a pool of n pictures total. We can restate the question 'How many pictures n do we need, so that we can construct a set of k cards with only one shared picture between any pair of cards?' equivalently by asking:

Given an n-dimensional vector space and the set of all vectors, which contain exactly m elements equal to one and all other zero, how big has n to be, so that we can find a set of k vectors, whose pairwise dot products are all equal to 1?

There are exactly (n choose m) possible vectors to build pairs from. So we at least need a big enough n so that (n choose m) >= k. This is just a lower bound, so for fulfilling the pairwise compatibility constraint we possibly need a much higher n.

Just for experimenting a bit i wrote a small Haskell program to calculate valid card sets:

Edit: I just realized after seeing Neil's and Gajet's solution, that the algorithm i use doesn't always find the best possible solution, so everything below isn't necessarily valid. I'll try to update my code soon.

module Main where

cardCandidates n m = cardCandidates' [] (n-m) m
cardCandidates' buildup  0  0 = [buildup]
cardCandidates' buildup zc oc
    | zc>0 && oc>0 = zerorec ++ onerec
    | zc>0         = zerorec
    | otherwise    = onerec
    where zerorec = cardCandidates' (0:buildup) (zc-1) oc
          onerec  = cardCandidates' (1:buildup) zc (oc-1)

dot x y = sum $ zipWith (*) x y
compatible x y = dot x y == 1

compatibleCards = compatibleCards' []
compatibleCards' valid     [] = valid
compatibleCards' valid (c:cs)
  | all (compatible c) valid = compatibleCards' (c:valid) cs
  |                otherwise = compatibleCards'    valid  cs

legalCardSet n m = compatibleCards $ cardCandidates n m

main = mapM_ print [(n, length $ legalCardSet n m) | n<-[m..]]
  where m = 8

The resulting maximum number of compatible cards for m=8 pictures per card for different number of pictures to choose from n for the first few n looks like this:

This brute force method doesn't get very far though because of combinatorial explosion. But i thought it might still be interesting.

Interestingly, it seems that for given m, k increases with n only up to a certain n, after which it stays constant.

This means, that for every number of pictures per card there is a certain number of pictures to choose from, that results in maximum possible number of legal cards. Adding more pictures to choose from past that optimal number doesn't increase the number of legal cards any further.

The first few optimal k's are:

Hayrack

That's just an initial attempt at a bound, right? You have not incorporated the "pairwise dot products equal to 1" requirement... – Perturbation

Apparently the syntax highlighter here doesn't really support Haskell yet (meta.stackexchange.com/questions/78363/…), but I'll toss in the hint just in case it does in future. – Chellman

@Chellman thanks for your edit! i didn't know you could give hints for language-specific syntax highlighting. – Hayrack

It's not very well-known yet :) – Chellman

Answer 4

Others have described the general framework for the design (finite projective plane) and shown how to generate finite projective planes of prime order. I would just like to fill in some gaps.

Finite projective planes can be generated for many different orders, but they are most straightforward in the case of prime order p. Then the integers modulo p form a finite field which can be used to describe coordinates for the points and lines in the plane. There are 3 different kinds of coordinates for points: (1,x,y), (0,1,x), and (0,0,1), where x and y can take on values from 0 to p-1. The 3 different kinds of points explains the formula p^2+p+1 for the number of points in the system. We can also describe lines with the same 3 different kinds of coordinates: [1,x,y], [0,1,x], and [0,0,1].

We compute whether a point and line are incident by whether the dot product of their coordinates is equal to 0 mod p. So for example the point (1,2,5) and the line [0,1,1] are incident when p=7 since 1*0+2*1+5*1 = 7 == 0 mod 7, but the point (1,3,3) and the line [1,2,6] are not incident since 1*1+3*2+3*6 = 25 != 0 mod 7.

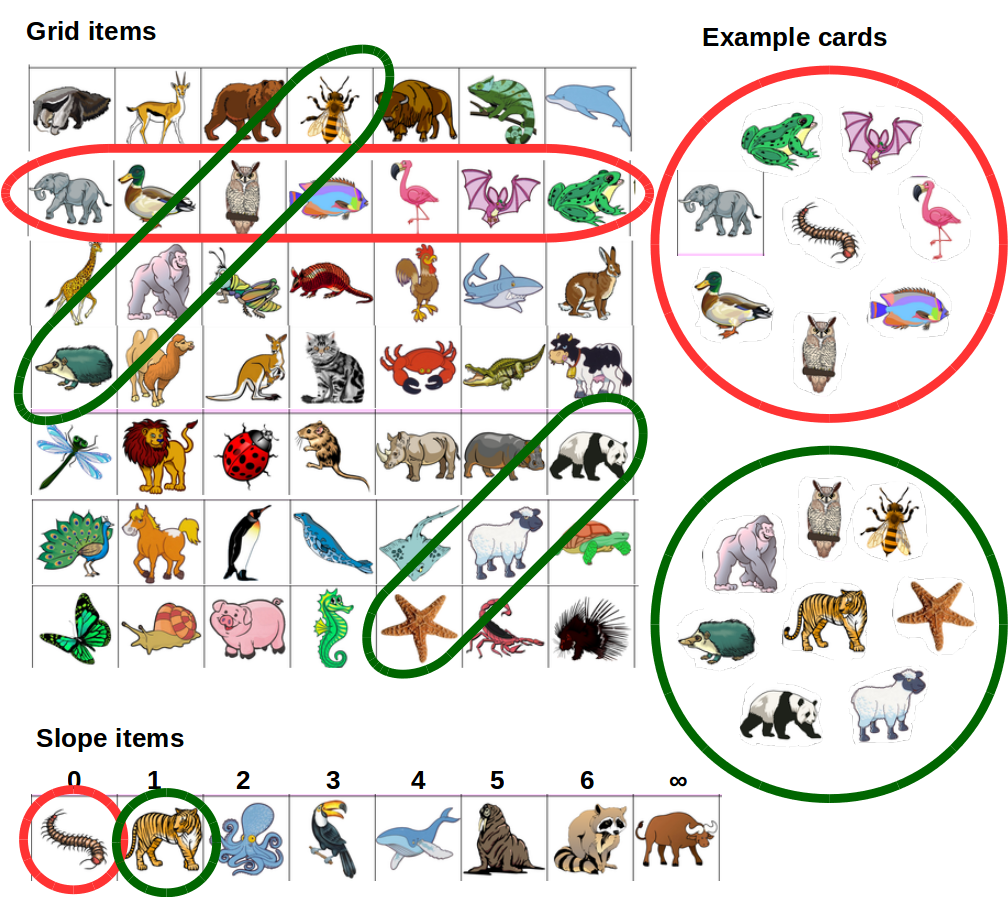
Translating into the language of cards and pictures, that means the picture with coordinates (1,2,5) is contained in the card with coordinates [0,1,1], but the picture with coordinates (1,3,3) is not contained in the card with coordinates [1,2,6]. We can use this procedure to develop a complete list of cards and the pictures that they contain.

I think it's easier to think of pictures as points and cards as lines, but there's a duality in projective geometry between points and lines so it really doesn't matter. However, in what follows I will be using points for pictures and lines for cards.

The same construction works for any finite field. We know that there is a finite field of order q if and only if q=p^k, a prime power. The field is called GF(p^k) which stands for "Galois field". The fields are not as easy to construct in the prime power case as they are in the prime case.

Fortunately, the hard work has already been done and implemented in free software, namely Sage Math. To get a projective plane design of order 4, for example, just type

PG = designs.ProjectiveGeometryDesign(2,1,GF(4),point_coordinates=0)
PG.blocks()

and you'll obtain output that looks like

[[0,1,2,3,20], [0,4,8,12,16], [0,5,10,15,19], [0,6,11,13,17],
 [0,7,9,14,18], [1,4,11,14,19], [1,5,9,13,16], [1,6,8,15,18],
 [1,7,10,12,17], [2,4,9,15,17], [2,5,11,12,18], [2,6,10,14,16],
 [2,7,8,13,19], [3,4,10,13,18], [3,5,8,14,17], [3,6,9,12,19],
 [3,7,11,15,16], [4,5,6,7,20], [8,9,10,11,20], [12,13,14,15,20],
 [16,17,18,19,20]]

I interpret the above as follows: there are 21 pictures labelled from 0 to 20. Each of the blocks (lines in projective geometry) tells me which pictures appears on a card. For example, the first card will have pictures 0, 1, 2, 3, and 20; the second card will have pictures 0, 4, 8, 12, and 16; and so on.

The system of order 7 can be generated by

PG = designs.ProjectiveGeometryDesign(2,1,GF(7),point_coordinates=0)
PG.blocks()

which generates the output

[[0, 1, 2, 3, 4, 5, 6, 56], [0, 7, 14, 21, 28, 35, 42, 49], 
[0, 8, 16, 24, 32, 40, 48, 50], [0, 9, 18, 27, 29, 38, 47, 51],
[0, 10, 20, 23, 33, 36, 46, 52], [0, 11, 15,
26, 30, 41, 45, 53], [0, 12, 17, 22, 34, 39, 44, 54], [0, 13, 19, 25,
31, 37, 43, 55], [1, 7, 20, 26, 32, 38, 44, 55], [1, 8, 15, 22, 29, 36,
43, 49], [1, 9, 17, 25, 33, 41, 42, 50], [1, 10, 19, 21, 30, 39, 48,
51], [1, 11, 14, 24, 34, 37, 47, 52], [1, 12, 16, 27, 31, 35, 46, 53],
[1, 13, 18, 23, 28, 40, 45, 54], [2, 7, 19, 24, 29, 41, 46, 54], [2, 8,
14, 27, 33, 39, 45, 55], [2, 9, 16, 23, 30, 37, 44, 49], [2, 10, 18, 26,
34, 35, 43, 50], [2, 11, 20, 22, 31, 40, 42, 51], [2, 12, 15, 25, 28,
38, 48, 52], [2, 13, 17, 21, 32, 36, 47, 53], [3, 7, 18, 22, 33, 37, 48,
53], [3, 8, 20, 25, 30, 35, 47, 54], [3, 9, 15, 21, 34, 40, 46, 55], [3,
10, 17, 24, 31, 38, 45, 49], [3, 11, 19, 27, 28, 36, 44, 50], [3, 12,
14, 23, 32, 41, 43, 51], [3, 13, 16, 26, 29, 39, 42, 52], [4, 7, 17, 27,
30, 40, 43, 52], [4, 8, 19, 23, 34, 38, 42, 53], [4, 9, 14, 26, 31, 36,
48, 54], [4, 10, 16, 22, 28, 41, 47, 55], [4, 11, 18, 25, 32, 39, 46,
49], [4, 12, 20, 21, 29, 37, 45, 50], [4, 13, 15, 24, 33, 35, 44, 51],
[5, 7, 16, 25, 34, 36, 45, 51], [5, 8, 18, 21, 31, 41, 44, 52], [5, 9,
20, 24, 28, 39, 43, 53], [5, 10, 15, 27, 32, 37, 42, 54], [5, 11, 17,
23, 29, 35, 48, 55], [5, 12, 19, 26, 33, 40, 47, 49], [5, 13, 14, 22,
30, 38, 46, 50], [6, 7, 15, 23, 31, 39, 47, 50], [6, 8, 17, 26, 28, 37,
46, 51], [6, 9, 19, 22, 32, 35, 45, 52], [6, 10, 14, 25, 29, 40, 44,
53], [6, 11, 16, 21, 33, 38, 43, 54], [6, 12, 18, 24, 30, 36, 42, 55],
[6, 13, 20, 27, 34, 41, 48, 49], [7, 8, 9, 10, 11, 12, 13, 56], [14, 15,
16, 17, 18, 19, 20, 56], [21, 22, 23, 24, 25, 26, 27, 56], [28, 29, 30,
31, 32, 33, 34, 56], [35, 36, 37, 38, 39, 40, 41, 56], [42, 43, 44, 45,
46, 47, 48, 56], [49, 50, 51, 52, 53, 54, 55, 56]]

If you want up to 57 cards you can use GF(7). If you want 58 cards you'll have to use a larger field. Since 8 is a power of a prime, you could use GF(8). Note that the projective plane based on GF(8) will have 8^2 + 8 + 1 = 73 points and 73 lines. You can make 73 cards, but then just throw away 15 of them if you want a set of exactly 58 cards. If you want between 73 and 91 cards you could use GF(9), etc. There is no GF(10) because 10 is not a power of a prime. GF(11) is next, then GF(13), then GF(16) because 16=2^4, and so on.

By the way, I have a theory that the original Spot It deck uses 55, not 57, because they contracted a playing card manufacturer which was already tooled for decks of 55 cards (52 regular cards in a deck, plus two jokers and a title card).

Communard

Answer 5

I just found a way to do it with 57 or 58 pictures but now I have a very bad headache, I'll post the ruby code in 8-10 hours after I slept well! just a hint my my solution every 7 cards share same mark and total 56 cards can be constructed using my solution.

here is the code that generates all 57 cards that ypercube was talking about. it uses exactly 57 pictures, and sorry guy's I've written actual C++ code but knowing that vector <something> is an array containing values of type something it's easy to understand what this code does. and this code generates P^2+P+1 cards using P^2+P+1 pictures each containing P+1 picture and sharing only 1 picture in common, for every prime P value. which means we can have 7 cards using 7 pictures each having 3 pictures(for p=2), 13 cards using 13 pictures(for p=3), 31 cards using 31 pictures(for p=5), 57 cards for 57 pictures(for p=7) and so on...

#include <iostream>
#include <vector>

using namespace std;

vector <vector<int> > cards;

void createcards(int p)
{
    cards.resize(0);
    for (int i=0;i<p;i++)
    {
        cards.resize(cards.size()+1);
        for(int j=0;j<p;j++)
        {
            cards.back().push_back(i*p+j);
        }
        cards.back().push_back(p*p+1);
    }

    for (int i=0;i<p;i++)
    {
        for(int j=0;j<p;j++)
        {
            cards.resize(cards.size()+1);
            for(int k=0;k<p;k++)
            {
                cards.back().push_back(k*p+(j+i*k)%p);
            }
            cards.back().push_back(p*p+2+i);
        }
    }

    cards.resize(cards.size()+1);

    for (int i=0;i<p+1;i++)
        cards.back().push_back(p*p+1+i);
}

void checkCards()
{
    cout << "---------------------\n";
    for(unsigned i=0;i<cards.size();i++)
    {
        for(unsigned j=0;j<cards[i].size();j++)
        {
            printf("%3d",cards[i][j]);
        }
        cout << "\n";
    }
    cout << "---------------------\n";
    for(unsigned i=0;i<cards.size();i++)
    {
        for(unsigned j=i+1;j<cards.size();j++)
        {
            int sim = 0;
            for(unsigned k=0;k<cards[i].size();k++)
                for(unsigned l=0;l<cards[j].size();l++)
                    if (cards[i][k] == cards[j][l])
                        sim ++;
            if (sim != 1)
                cout << "there is a problem between cards : " << i << " " << j << "\n";

        }
    }
}

int main()
{
    int p;
    for(cin >> p; p!=0;cin>> p)
    {
        createcards(p);
        checkCards();
    }
}

again sorry for the delayed code.

Playground

I have an elegant proof of this, but alas this comment box is too small to contain it. – Indefinable

@Gajet: Did you run it for p=4? (and 21 cards/pictures) – Archerfish

4 isn't doesn't work in my algorithm since 4 is not a prime number, in my algorithm it's important that p should be prime. – Playground

@ypercube after checking again there was some minior mistakes in my algorithm but i checked it for, 2 ,3,5,7 and I can prove for any other prime number it will work, so here is my complete code (but in c++) – Playground

@Gajet: Nice work. Just curious if it also solves the prime powers cases: 4, 8, 9, 16, .... – Archerfish

@Gajet: I also ported your solution to Python to check it/understand it. I hope you don't mind. Feel free to move the ported code from my answer to yours if you want to. – Kermis

@Gajet: I also found a bug in your code: You never create card p*p. You can shift down some indices by 1. – Kermis

@Neil G: you are right, now you mention it i just wrote half of the code numbering from 0 to p^2+p and the other half numbering from 1 to p^2+p+1, that's why I skiped p*p. but i don't call that a bug specificly! and you upvoted after I mentioned it when i said you didn't it still had 2 votes! :D – Playground

@Gajet: I also fixed your algorithm so that it works with non-prime numbers. Please let me know if it looks right to you. – Kermis

@neil : do you mean in your code or in mine? since mine doesn't seem to be changed at all. – Playground

@Gajet: cool solution! Now i get why my greedy algorithm didn't always produce the best solution. – Hayrack

Answer 6

Here's Gajet's solution in Python, since I find Python more readable. I have modified it so that it works with non-prime numbers as well. I have used Thies insight to generate some more easily understood display code.

from __future__ import print_function
from itertools import *

def create_cards(p):
    for min_factor in range(2, 1 + int(p ** 0.5)):
        if p % min_factor == 0:
            break
    else:
        min_factor = p
    cards = []
    for i in range(p):
        cards.append(set([i * p + j for j in range(p)] + [p * p]))
    for i in range(min_factor):
        for j in range(p):
            cards.append(set([k * p + (j + i * k) % p
                              for k in range(p)] + [p * p + 1 + i]))

    cards.append(set([p * p + i for i in range(min_factor + 1)]))
    return cards, p * p + p + 1

def display_using_stars(cards, num_pictures):
    for pictures_for_card in cards:
        print("".join('*' if picture in pictures_for_card else ' '
                      for picture in range(num_pictures)))

def check_cards(cards):
    for card, other_card in combinations(cards, 2):
        if len(card & other_card) != 1:
            print("Cards", sorted(card), "and", sorted(other_card),
                  "have intersection", sorted(card & other_card))

cards, num_pictures = create_cards(7)
display_using_stars(cards, num_pictures)
check_cards(cards)

With output:

***      *   
   ***   *   
      ****   
*  *  *   *  
 *  *  *  *  
  *  *  * *  
*   *   *  * 
 *   **    * 
  **   *   * 
*    * *    *
 * *    *   *
  * * *     *
         ****

Kermis

glad that you found the idea helpful. I like the illustration of the card set. – Hayrack

i think the last three cards in your example aren't valid, because they don't share a picture with the fifth card. Just checked my code for over an hour before i realized it :) Interestingly, it seems the maximum size of a legal cardset is 5 for 4 pictures per card and doesn't increase even with more pictures to choose from. – Hayrack

@Thies: Nice catch. Looks like this greedy algorithm doesn't work. My next approach is to do it recursively. – Kermis

@Neil: Looking forward to see what you come up with. I'll also try to do a new version of my code since the current one is kind of wasteful and therefore only feasible for small sizes at the moment. – Hayrack

@Neil: Nice. Theory says that with PICTURES_PER_CARD = 4, you could have an arrangement of 3^2+3+1 = 13 cards and 13 pictures. – Archerfish

@ypercube: that's interesting. Does the theory predict that there definitely should be 13 cards and pictures? because from my experiments it seems like this is just an upper bound that isn't reached in every case (e.g. for 4 pictures per card i got a maximum of 5 different cards with 10 pictures). – Hayrack

@Thies: No, there are other arrangements, if you keep only the first axiom/condition: Given any 2 cards chosen from the deck, there is 1 and only 1 matching picture and not the second Given two pictures there is exactly 1 card that has both of them. The problem has connections with combinatorial block design, coding theory (like error-correction codes) and probably other areas of mathematics/computer science. – Archerfish

@Thies with the diagram I produced using Gajet's code, it's much easier to see why there are exactly (p) + (p * p) + (1) configurations. – Kermis

@NeilG: I think in your algorithm all the cards generated are valid but for non prime values of p, there are less than p*p+p+1 cards generated. – Playground

@Gajet: Exactly. Is it really possible to have all p*p + p + 1 cards in those cases? – Kermis

@NeilG: As i explained to ypercube in my comments I think it's possible to generate for all p except 4 and 6. i'm refering to an axiom in ring theory, and the key is to change multiplication operator in k * p + (j + i * k) % p between i and k; – Playground

@Neil: Thanks for the updated diagram, makes it much easier to see how Gajet's solution works! – Hayrack

@Gajet: I think you are wrong about all p except 4 and 6. If you want to produce a finite plane where there are p*p+p+1 points and lines (cards and pictures), then it's related to finite fields and not rings. There are finite fields of order p when p is prime or a prime power. Your code works correctly for primes because expressions like k * p + (j + i * k) % p are expressing k*p + j + i*k in terms of the multiplication and addition in the finite field of order p. – Archerfish

It will work correctly for prime powers too, if you can express these operations (mult. and addition) in the finite fields of order p^2, p^3, etc. So, it will work for 4, 8, 9, 16, 25, 27, ... – Archerfish

@ypercube: What is the solution for 4? Because this solution doesn't work for 4. – Kermis

@tpercube: yes i was rwong about 4 and 6, after more research it seems it can work at elast for any p^k, now i'm developing an algorithm that can handle addition and multiplication of p^k elements. right now i'm stuck with mutiplication, you can check math forum to see how I'm trying to construct these two operators. – Playground

Answer 7

Using the z3 theorem prover

Let P be the number of symbols per card. According to this article and ypercubeᵀᴹ's answer there are N = P**2 - P + 1 cards and symbols, respectively. A deck of cards can be represented with its incidence matrix which has a row for each card and a column for each possible symbol. Its (i,j) element is 1 if card i has symbol j on it. We only need to fill this matrix with these constraints in mind:

• every element is either zero or one
• the sum of each row is exactly P
• the sum of each column is exactly P
• any two rows must have exactly one symbol in common

That means N**2 variables and N**2 + 2*N + (N choose 2) constraints. It seems to be manageable in a not-so-long time with z3 for small inputs.

edit: Unfortunately P=8 seems to be too big for this method. I killed the process after 14 hour of computation time.

from z3 import *
from itertools import combinations

def is_prime_exponent(K):
    return K > 1 and K not in 6  # next non-prime exponent is 10, 
                                 # but that is too big anyway

def transposed(rows):
    return zip(*rows)

def spotit_z3(symbols_per_card):
    K = symbols_per_card - 1
    N = symbols_per_card ** 2 - symbols_per_card + 1
    if not is_prime_exponent(K):
        raise TypeError("Symbols per card must be a prime exponent plus one.")

    constraints = []

    # the rows of the incidence matrix
    s = N.bit_length()
    rows = [[BitVec("r%dc%d" % (r, c), s) for c in range(N)] for r in range(N)]

    # every element must be either 1 or 0
    constraints += [Or([elem == 1, elem == 0]) for row in rows for elem in row]

    # sum of rows and cols must be exactly symbols_per_card
    constraints += [Sum(row) == symbols_per_card for row in rows]
    constraints += [Sum(col) == symbols_per_card for col in transposed(rows)]

    # Any two rows must have exactly one symbol in common, in other words they
    # differ in (symbols_per_card - 1) symbols, so their element-wise XOR will
    # have 2 * (symbols_per_card - 1) ones.
    D = 2 * (symbols_per_card - 1)
    for row_a, row_b in combinations(rows, 2):
        constraints += [Sum([a ^ b for a, b in zip(row_a, row_b)]) == D]

    solver = Solver()
    solver.add(constraints)

    if solver.check() == unsat:
        raise RuntimeError("Could not solve it :(")

    # create the incidence matrix
    model = solver.model()
    return [[model[elem].as_long() for elem in row] for row in rows]


if __name__ == "__main__":
    import sys
    symbols_per_card = int(sys.argv[1])
    incidence_matrix = spotit_z3(symbols_per_card)
    for row in incidence_matrix:
        print(row)

Results

$python spotit_z3.py 3
[0, 0, 1, 1, 0, 1, 0]
[0, 0, 0, 0, 1, 1, 1]
[0, 1, 0, 1, 0, 0, 1]
[1, 1, 0, 0, 0, 1, 0]
[0, 1, 1, 0, 1, 0, 0]
[1, 0, 0, 1, 1, 0, 0]
[1, 0, 1, 0, 0, 0, 1]
python spotit_z3.py 3  1.12s user 0.06s system 96% cpu 1.225 total

$ time python3 spotit_z3.py 4
[0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0, 1, 0]
[0, 0, 0, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0]
[0, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 0, 1]
[0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0]        
[0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1]
[0, 0, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0]
[0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1]
[0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 0]
[0, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0]
[1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1]
[1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0]
[1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0]
[1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0]
python spotit_z3.py 4  664.62s user 0.15s system 99% cpu 11:04.88 total

$ time python3 spotit_z3.py 5
[1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0]
[0, 0, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0]
[0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0]
[0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1]
[0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0]
[0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0]
[0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1]
[1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0]
[0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0]
[0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0]
[0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1]
[1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1]
[1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0]
[0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0]
[0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1]
[1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0]
python spotit_z3.py 5  1162.72s user 20.34s system 99% cpu 19:43.39 total

$ time python3 spotit_z3.py 8
<I killed it after 14 hours of run time.>

Mithgarthr

Answer 8

I very much like this thread. I build this github python project with parts of this code here to draw custom cards as png (so one can order custom card games in the internet).

https://github.com/plagtag/ProjectiveGeometry-Game

Blume

Answer 9

I wrote an article about how to generate this kind of decks, with code in Perl. The code is not optimized but it's at least capable of generating decks of "reasonable" orders... and some more.

Here's an example with order 8, which has to consider a slightly more complicated underlying math, because 8 is not prime although a valid order for generating these kind of decks. See above or the article for a more detailed explanation, below if you just want to generate a slightly more difficult Spot-It :-)

$ time pg2 8
elements in field: 8
  0. (1, 9, 17, 25, 33, 41, 49, 57, 65)
  1. (0, 9, 10, 11, 12, 13, 14, 15, 16)
  2. (2, 9, 18, 27, 36, 45, 54, 63, 72)
  3. (6, 9, 22, 26, 37, 43, 56, 60, 71)
  4. (7, 9, 23, 32, 34, 46, 52, 59, 69)
  5. (8, 9, 24, 30, 35, 42, 55, 61, 68)
  6. (3, 9, 19, 29, 39, 44, 50, 64, 70)
  7. (4, 9, 20, 31, 38, 48, 53, 58, 67)
  8. (5, 9, 21, 28, 40, 47, 51, 62, 66)
  9. (0, 1, 2, 3, 4, 5, 6, 7, 8)
 10. (1, 10, 18, 26, 34, 42, 50, 58, 66)
 11. (1, 14, 22, 30, 38, 46, 54, 62, 70)
 12. (1, 15, 23, 31, 39, 47, 55, 63, 71)
 13. (1, 16, 24, 32, 40, 48, 56, 64, 72)
 14. (1, 11, 19, 27, 35, 43, 51, 59, 67)
 15. (1, 12, 20, 28, 36, 44, 52, 60, 68)
 16. (1, 13, 21, 29, 37, 45, 53, 61, 69)
 17. (0, 17, 18, 19, 20, 21, 22, 23, 24)
 18. (2, 10, 17, 28, 35, 46, 53, 64, 71)
 19. (6, 14, 17, 29, 34, 48, 51, 63, 68)
 20. (7, 15, 17, 26, 40, 44, 54, 61, 67)
 21. (8, 16, 17, 27, 38, 47, 50, 60, 69)
 22. (3, 11, 17, 31, 37, 42, 52, 62, 72)
 23. (4, 12, 17, 30, 39, 45, 56, 59, 66)
 24. (5, 13, 17, 32, 36, 43, 55, 58, 70)
 25. (0, 49, 50, 51, 52, 53, 54, 55, 56)
 26. (3, 10, 20, 30, 40, 43, 49, 63, 69)
 27. (2, 14, 21, 32, 39, 42, 49, 60, 67)
 28. (8, 15, 18, 28, 37, 48, 49, 59, 70)
 29. (6, 16, 19, 31, 36, 46, 49, 61, 66)
 30. (5, 11, 23, 26, 38, 45, 49, 64, 68)
 31. (7, 12, 22, 29, 35, 47, 49, 58, 72)
 32. (4, 13, 24, 27, 34, 44, 49, 62, 71)
 33. (0, 57, 58, 59, 60, 61, 62, 63, 64)
 34. (4, 10, 19, 32, 37, 47, 54, 57, 68)
 35. (5, 14, 18, 31, 35, 44, 56, 57, 69)
 36. (2, 15, 24, 29, 38, 43, 52, 57, 66)
 37. (3, 16, 22, 28, 34, 45, 55, 57, 67)
 38. (7, 11, 21, 30, 36, 48, 50, 57, 71)
 39. (6, 12, 23, 27, 40, 42, 53, 57, 70)
 40. (8, 13, 20, 26, 39, 46, 51, 57, 72)
 41. (0, 65, 66, 67, 68, 69, 70, 71, 72)
 42. (5, 10, 22, 27, 39, 48, 52, 61, 65)
 43. (3, 14, 24, 26, 36, 47, 53, 59, 65)
 44. (6, 15, 20, 32, 35, 45, 50, 62, 65)
 45. (2, 16, 23, 30, 37, 44, 51, 58, 65)
 46. (4, 11, 18, 29, 40, 46, 55, 60, 65)
 47. (8, 12, 21, 31, 34, 43, 54, 64, 65)
 48. (7, 13, 19, 28, 38, 42, 56, 63, 65)
 49. (0, 25, 26, 27, 28, 29, 30, 31, 32)
 50. (6, 10, 21, 25, 38, 44, 55, 59, 72)
 51. (8, 14, 19, 25, 40, 45, 52, 58, 71)
 52. (4, 15, 22, 25, 36, 42, 51, 64, 69)
 53. (7, 16, 18, 25, 39, 43, 53, 62, 68)
 54. (2, 11, 20, 25, 34, 47, 56, 61, 70)
 55. (5, 12, 24, 25, 37, 46, 50, 63, 67)
 56. (3, 13, 23, 25, 35, 48, 54, 60, 66)
 57. (0, 33, 34, 35, 36, 37, 38, 39, 40)
 58. (7, 10, 24, 31, 33, 45, 51, 60, 70)
 59. (4, 14, 23, 28, 33, 43, 50, 61, 72)
 60. (3, 15, 21, 27, 33, 46, 56, 58, 68)
 61. (5, 16, 20, 29, 33, 42, 54, 59, 71)
 62. (8, 11, 22, 32, 33, 44, 53, 63, 66)
 63. (2, 12, 19, 26, 33, 48, 55, 62, 69)
 64. (6, 13, 18, 30, 33, 47, 52, 64, 67)
 65. (0, 41, 42, 43, 44, 45, 46, 47, 48)
 66. (8, 10, 23, 29, 36, 41, 56, 62, 67)
 67. (7, 14, 20, 27, 37, 41, 55, 64, 66)
 68. (5, 15, 19, 30, 34, 41, 53, 60, 72)
 69. (4, 16, 21, 26, 35, 41, 52, 63, 70)
 70. (6, 11, 24, 28, 39, 41, 54, 58, 69)
 71. (3, 12, 18, 32, 38, 41, 51, 61, 71)
 72. (2, 13, 22, 31, 40, 41, 50, 59, 68)
errors in check: 0

real    0m0.303s
user    0m0.200s
sys 0m0.016s

Each identifier from 0 to 72 can be read both as a card identifier and as a picture identifier. For example, the last row means that:

• card 72 contains pictures 2, 13, 22, ..., 59, 68, AND
• picture 72 appears in cards 2, 13, 22, ..., 59, and 68.

Overarm

Answer 10

I wrote the following code to calculate the cards. The idea is to create the first card with n images on it. If the difference of every pair of image indexes is unique then the rest of the cards can be generated trivially, by increasing each index with the same value modulo m = n * n - n + 1

static public int[] Backtrack(int n)
        {
            int m = n * n - n + 1;
            int[] Check = new int[m];
            int C = 1;
            int[] T = new int[n];
            int _p = 2;
            T[1] = 1;
            if (n > 2) T[2] = 1;
            else return T;
            while (_p >= 2)
            {
                T[_p]++;
                if (T[_p] == m)
                {
                    _p--;
                    continue;
                }
                bool good = true;
                C++;
                for (int i = 0; i <= _p; i++)
                {
                    for (int j = 0; j < i; j++)
                    {
                        int x = (T[i] - T[j] + m) % m;
                        if (Check[x] == C || Check[m - x] == C)//x cannot be equal to m-x as m is odd.
                            good = false;
                        Check[m - x] = C;
                        Check[x] = C;
                    }
                }
                if (good)
                {
                    _p++;
                    if (_p == n)
                    {
                        _p--;
                        return T;
                    }
                    T[_p] = T[_p - 1];
                }

            }
            return new int[] { };
        }
        static void Main(string[] args)
        {
            for (int N = 2; N < 11; N++)
            {
                var X = Backtrack(N);
                if (X.Length > 0)
                {
                    int K = N * N - N + 1;
                    Console.WriteLine("Cards: {0} Order {1}:", K, N - 1);
                    int C = 0;
                    for (int j = 0; j < K; j++)
                    {
                        Console.Write("Card {0:000}:", C++);
                        for (int i = 0; i < N; i++)
                        {
                            var t = (X[i] + j) % K;
                            if (j != 0 && Array.Exists(X, x => (x == t)))
                                Console.ForegroundColor = ConsoleColor.Green;
                            Console.Write("\t{0}", t);
                            Console.ResetColor();
                        }
                        Console.WriteLine();
                    }
                }

            }
        }

output:

Cards: 3 Order 1:
Card 000:   0   1
Card 001:   1   2
Card 002:   2   0
Cards: 7 Order 2:
Card 000:   0   1   3
Card 001:   1   2   4
Card 002:   2   3   5
Card 003:   3   4   6
Card 004:   4   5   0
Card 005:   5   6   1
Card 006:   6   0   2
Cards: 13 Order 3:
Card 000:   0   1   3   9
Card 001:   1   2   4   10
Card 002:   2   3   5   11
Card 003:   3   4   6   12
Card 004:   4   5   7   0
Card 005:   5   6   8   1
Card 006:   6   7   9   2
Card 007:   7   8   10  3
Card 008:   8   9   11  4
Card 009:   9   10  12  5
Card 010:   10  11  0   6
Card 011:   11  12  1   7
Card 012:   12  0   2   8
Cards: 21 Order 4:
Card 000:   0   1   4   14  16
Card 001:   1   2   5   15  17
Card 002:   2   3   6   16  18
Card 003:   3   4   7   17  19
Card 004:   4   5   8   18  20
Card 005:   5   6   9   19  0
Card 006:   6   7   10  20  1
Card 007:   7   8   11  0   2
Card 008:   8   9   12  1   3
Card 009:   9   10  13  2   4
Card 010:   10  11  14  3   5
Card 011:   11  12  15  4   6
Card 012:   12  13  16  5   7
Card 013:   13  14  17  6   8
Card 014:   14  15  18  7   9
Card 015:   15  16  19  8   10
Card 016:   16  17  20  9   11
Card 017:   17  18  0   10  12
Card 018:   18  19  1   11  13
Card 019:   19  20  2   12  14
Card 020:   20  0   3   13  15
Cards: 31 Order 5:
Card 000:   0   1   3   8   12  18
Card 001:   1   2   4   9   13  19
Card 002:   2   3   5   10  14  20
Card 003:   3   4   6   11  15  21
Card 004:   4   5   7   12  16  22
Card 005:   5   6   8   13  17  23
Card 006:   6   7   9   14  18  24
Card 007:   7   8   10  15  19  25
Card 008:   8   9   11  16  20  26
Card 009:   9   10  12  17  21  27
Card 010:   10  11  13  18  22  28
Card 011:   11  12  14  19  23  29
Card 012:   12  13  15  20  24  30
Card 013:   13  14  16  21  25  0
Card 014:   14  15  17  22  26  1
Card 015:   15  16  18  23  27  2
Card 016:   16  17  19  24  28  3
Card 017:   17  18  20  25  29  4
Card 018:   18  19  21  26  30  5
Card 019:   19  20  22  27  0   6
Card 020:   20  21  23  28  1   7
Card 021:   21  22  24  29  2   8
Card 022:   22  23  25  30  3   9
Card 023:   23  24  26  0   4   10
Card 024:   24  25  27  1   5   11
Card 025:   25  26  28  2   6   12
Card 026:   26  27  29  3   7   13
Card 027:   27  28  30  4   8   14
Card 028:   28  29  0   5   9   15
Card 029:   29  30  1   6   10  16
Card 030:   30  0   2   7   11  17
Cards: 57 Order 7:
Card 000:   0   1   3   13  32  36  43  52
Card 001:   1   2   4   14  33  37  44  53
Card 002:   2   3   5   15  34  38  45  54
Card 003:   3   4   6   16  35  39  46  55
Card 004:   4   5   7   17  36  40  47  56
Card 005:   5   6   8   18  37  41  48  0
Card 006:   6   7   9   19  38  42  49  1
Card 007:   7   8   10  20  39  43  50  2
Card 008:   8   9   11  21  40  44  51  3
Card 009:   9   10  12  22  41  45  52  4
Card 010:   10  11  13  23  42  46  53  5
Card 011:   11  12  14  24  43  47  54  6
Card 012:   12  13  15  25  44  48  55  7
Card 013:   13  14  16  26  45  49  56  8
Card 014:   14  15  17  27  46  50  0   9
Card 015:   15  16  18  28  47  51  1   10
Card 016:   16  17  19  29  48  52  2   11
Card 017:   17  18  20  30  49  53  3   12
Card 018:   18  19  21  31  50  54  4   13
Card 019:   19  20  22  32  51  55  5   14
Card 020:   20  21  23  33  52  56  6   15
Card 021:   21  22  24  34  53  0   7   16
Card 022:   22  23  25  35  54  1   8   17
Card 023:   23  24  26  36  55  2   9   18
Card 024:   24  25  27  37  56  3   10  19
Card 025:   25  26  28  38  0   4   11  20
Card 026:   26  27  29  39  1   5   12  21
Card 027:   27  28  30  40  2   6   13  22
Card 028:   28  29  31  41  3   7   14  23
Card 029:   29  30  32  42  4   8   15  24
Card 030:   30  31  33  43  5   9   16  25
Card 031:   31  32  34  44  6   10  17  26
Card 032:   32  33  35  45  7   11  18  27
Card 033:   33  34  36  46  8   12  19  28
Card 034:   34  35  37  47  9   13  20  29
Card 035:   35  36  38  48  10  14  21  30
Card 036:   36  37  39  49  11  15  22  31
Card 037:   37  38  40  50  12  16  23  32
Card 038:   38  39  41  51  13  17  24  33
Card 039:   39  40  42  52  14  18  25  34
Card 040:   40  41  43  53  15  19  26  35
Card 041:   41  42  44  54  16  20  27  36
Card 042:   42  43  45  55  17  21  28  37
Card 043:   43  44  46  56  18  22  29  38
Card 044:   44  45  47  0   19  23  30  39
Card 045:   45  46  48  1   20  24  31  40
Card 046:   46  47  49  2   21  25  32  41
Card 047:   47  48  50  3   22  26  33  42
Card 048:   48  49  51  4   23  27  34  43
Card 049:   49  50  52  5   24  28  35  44
Card 050:   50  51  53  6   25  29  36  45
Card 051:   51  52  54  7   26  30  37  46
Card 052:   52  53  55  8   27  31  38  47
Card 053:   53  54  56  9   28  32  39  48
Card 054:   54  55  0   10  29  33  40  49
Card 055:   55  56  1   11  30  34  41  50
Card 056:   56  0   2   12  31  35  42  51
Cards: 73 Order 8:
Card 000:   0   1   3   7   15  31  36  54  63
Card 001:   1   2   4   8   16  32  37  55  64
Card 002:   2   3   5   9   17  33  38  56  65
Card 003:   3   4   6   10  18  34  39  57  66
Card 004:   4   5   7   11  19  35  40  58  67
Card 005:   5   6   8   12  20  36  41  59  68
Card 006:   6   7   9   13  21  37  42  60  69
Card 007:   7   8   10  14  22  38  43  61  70
Card 008:   8   9   11  15  23  39  44  62  71
Card 009:   9   10  12  16  24  40  45  63  72
Card 010:   10  11  13  17  25  41  46  64  0
Card 011:   11  12  14  18  26  42  47  65  1
Card 012:   12  13  15  19  27  43  48  66  2
Card 013:   13  14  16  20  28  44  49  67  3
Card 014:   14  15  17  21  29  45  50  68  4
Card 015:   15  16  18  22  30  46  51  69  5
Card 016:   16  17  19  23  31  47  52  70  6
Card 017:   17  18  20  24  32  48  53  71  7
Card 018:   18  19  21  25  33  49  54  72  8
Card 019:   19  20  22  26  34  50  55  0   9
Card 020:   20  21  23  27  35  51  56  1   10
Card 021:   21  22  24  28  36  52  57  2   11
Card 022:   22  23  25  29  37  53  58  3   12
Card 023:   23  24  26  30  38  54  59  4   13
Card 024:   24  25  27  31  39  55  60  5   14
Card 025:   25  26  28  32  40  56  61  6   15
Card 026:   26  27  29  33  41  57  62  7   16
Card 027:   27  28  30  34  42  58  63  8   17
Card 028:   28  29  31  35  43  59  64  9   18
Card 029:   29  30  32  36  44  60  65  10  19
Card 030:   30  31  33  37  45  61  66  11  20
Card 031:   31  32  34  38  46  62  67  12  21
Card 032:   32  33  35  39  47  63  68  13  22
Card 033:   33  34  36  40  48  64  69  14  23
Card 034:   34  35  37  41  49  65  70  15  24
Card 035:   35  36  38  42  50  66  71  16  25
Card 036:   36  37  39  43  51  67  72  17  26
Card 037:   37  38  40  44  52  68  0   18  27
Card 038:   38  39  41  45  53  69  1   19  28
Card 039:   39  40  42  46  54  70  2   20  29
Card 040:   40  41  43  47  55  71  3   21  30
Card 041:   41  42  44  48  56  72  4   22  31
Card 042:   42  43  45  49  57  0   5   23  32
Card 043:   43  44  46  50  58  1   6   24  33
Card 044:   44  45  47  51  59  2   7   25  34
Card 045:   45  46  48  52  60  3   8   26  35
Card 046:   46  47  49  53  61  4   9   27  36
Card 047:   47  48  50  54  62  5   10  28  37
Card 048:   48  49  51  55  63  6   11  29  38
Card 049:   49  50  52  56  64  7   12  30  39
Card 050:   50  51  53  57  65  8   13  31  40
Card 051:   51  52  54  58  66  9   14  32  41
Card 052:   52  53  55  59  67  10  15  33  42
Card 053:   53  54  56  60  68  11  16  34  43
Card 054:   54  55  57  61  69  12  17  35  44
Card 055:   55  56  58  62  70  13  18  36  45
Card 056:   56  57  59  63  71  14  19  37  46
Card 057:   57  58  60  64  72  15  20  38  47
Card 058:   58  59  61  65  0   16  21  39  48
Card 059:   59  60  62  66  1   17  22  40  49
Card 060:   60  61  63  67  2   18  23  41  50
Card 061:   61  62  64  68  3   19  24  42  51
Card 062:   62  63  65  69  4   20  25  43  52
Card 063:   63  64  66  70  5   21  26  44  53
Card 064:   64  65  67  71  6   22  27  45  54
Card 065:   65  66  68  72  7   23  28  46  55
Card 066:   66  67  69  0   8   24  29  47  56
Card 067:   67  68  70  1   9   25  30  48  57
Card 068:   68  69  71  2   10  26  31  49  58
Card 069:   69  70  72  3   11  27  32  50  59
Card 070:   70  71  0   4   12  28  33  51  60
Card 071:   71  72  1   5   13  29  34  52  61
Card 072:   72  0   2   6   14  30  35  53  62
Cards: 91 Order 9:
Card 000:   0   1   3   9   27  49  56  61  77  81
Card 001:   1   2   4   10  28  50  57  62  78  82
Card 002:   2   3   5   11  29  51  58  63  79  83
Card 003:   3   4   6   12  30  52  59  64  80  84
Card 004:   4   5   7   13  31  53  60  65  81  85
Card 005:   5   6   8   14  32  54  61  66  82  86
Card 006:   6   7   9   15  33  55  62  67  83  87
Card 007:   7   8   10  16  34  56  63  68  84  88
Card 008:   8   9   11  17  35  57  64  69  85  89
Card 009:   9   10  12  18  36  58  65  70  86  90
Card 010:   10  11  13  19  37  59  66  71  87  0
Card 011:   11  12  14  20  38  60  67  72  88  1
Card 012:   12  13  15  21  39  61  68  73  89  2
Card 013:   13  14  16  22  40  62  69  74  90  3
Card 014:   14  15  17  23  41  63  70  75  0   4
Card 015:   15  16  18  24  42  64  71  76  1   5
Card 016:   16  17  19  25  43  65  72  77  2   6
Card 017:   17  18  20  26  44  66  73  78  3   7
Card 018:   18  19  21  27  45  67  74  79  4   8
Card 019:   19  20  22  28  46  68  75  80  5   9
Card 020:   20  21  23  29  47  69  76  81  6   10
Card 021:   21  22  24  30  48  70  77  82  7   11
Card 022:   22  23  25  31  49  71  78  83  8   12
Card 023:   23  24  26  32  50  72  79  84  9   13
Card 024:   24  25  27  33  51  73  80  85  10  14
Card 025:   25  26  28  34  52  74  81  86  11  15
Card 026:   26  27  29  35  53  75  82  87  12  16
Card 027:   27  28  30  36  54  76  83  88  13  17
Card 028:   28  29  31  37  55  77  84  89  14  18
Card 029:   29  30  32  38  56  78  85  90  15  19
Card 030:   30  31  33  39  57  79  86  0   16  20
Card 031:   31  32  34  40  58  80  87  1   17  21
Card 032:   32  33  35  41  59  81  88  2   18  22
Card 033:   33  34  36  42  60  82  89  3   19  23
Card 034:   34  35  37  43  61  83  90  4   20  24
Card 035:   35  36  38  44  62  84  0   5   21  25
Card 036:   36  37  39  45  63  85  1   6   22  26
Card 037:   37  38  40  46  64  86  2   7   23  27
Card 038:   38  39  41  47  65  87  3   8   24  28
Card 039:   39  40  42  48  66  88  4   9   25  29
Card 040:   40  41  43  49  67  89  5   10  26  30
Card 041:   41  42  44  50  68  90  6   11  27  31
Card 042:   42  43  45  51  69  0   7   12  28  32
Card 043:   43  44  46  52  70  1   8   13  29  33
Card 044:   44  45  47  53  71  2   9   14  30  34
Card 045:   45  46  48  54  72  3   10  15  31  35
Card 046:   46  47  49  55  73  4   11  16  32  36
Card 047:   47  48  50  56  74  5   12  17  33  37
Card 048:   48  49  51  57  75  6   13  18  34  38
Card 049:   49  50  52  58  76  7   14  19  35  39
Card 050:   50  51  53  59  77  8   15  20  36  40
Card 051:   51  52  54  60  78  9   16  21  37  41
Card 052:   52  53  55  61  79  10  17  22  38  42
Card 053:   53  54  56  62  80  11  18  23  39  43
Card 054:   54  55  57  63  81  12  19  24  40  44
Card 055:   55  56  58  64  82  13  20  25  41  45
Card 056:   56  57  59  65  83  14  21  26  42  46
Card 057:   57  58  60  66  84  15  22  27  43  47
Card 058:   58  59  61  67  85  16  23  28  44  48
Card 059:   59  60  62  68  86  17  24  29  45  49
Card 060:   60  61  63  69  87  18  25  30  46  50
Card 061:   61  62  64  70  88  19  26  31  47  51
Card 062:   62  63  65  71  89  20  27  32  48  52
Card 063:   63  64  66  72  90  21  28  33  49  53
Card 064:   64  65  67  73  0   22  29  34  50  54
Card 065:   65  66  68  74  1   23  30  35  51  55
Card 066:   66  67  69  75  2   24  31  36  52  56
Card 067:   67  68  70  76  3   25  32  37  53  57
Card 068:   68  69  71  77  4   26  33  38  54  58
Card 069:   69  70  72  78  5   27  34  39  55  59
Card 070:   70  71  73  79  6   28  35  40  56  60
Card 071:   71  72  74  80  7   29  36  41  57  61
Card 072:   72  73  75  81  8   30  37  42  58  62
Card 073:   73  74  76  82  9   31  38  43  59  63
Card 074:   74  75  77  83  10  32  39  44  60  64
Card 075:   75  76  78  84  11  33  40  45  61  65
Card 076:   76  77  79  85  12  34  41  46  62  66
Card 077:   77  78  80  86  13  35  42  47  63  67
Card 078:   78  79  81  87  14  36  43  48  64  68
Card 079:   79  80  82  88  15  37  44  49  65  69
Card 080:   80  81  83  89  16  38  45  50  66  70
Card 081:   81  82  84  90  17  39  46  51  67  71
Card 082:   82  83  85  0   18  40  47  52  68  72
Card 083:   83  84  86  1   19  41  48  53  69  73
Card 084:   84  85  87  2   20  42  49  54  70  74
Card 085:   85  86  88  3   21  43  50  55  71  75
Card 086:   86  87  89  4   22  44  51  56  72  76
Card 087:   87  88  90  5   23  45  52  57  73  77
Card 088:   88  89  0   6   24  46  53  58  74  78
Card 089:   89  90  1   7   25  47  54  59  75  79
Card 090:   90  0   2   8   26  48  55  60  76  80

Ablative