Documentation says this:
If maxsize is set to None, the LRU feature is disabled and the cache can grow without bound. The LRU feature performs best when maxsize is a power-of-two.
Would anyone happen to know where does this "power-of-two" come from? I am guessing it has something to do with the implementation.
I've long since removed the power-of-two suggestion from the docs because 1) with the current dict grow rate, the effect is minimal and 2) because the optimal maxsize should been 2**n * 2//3 + 1.
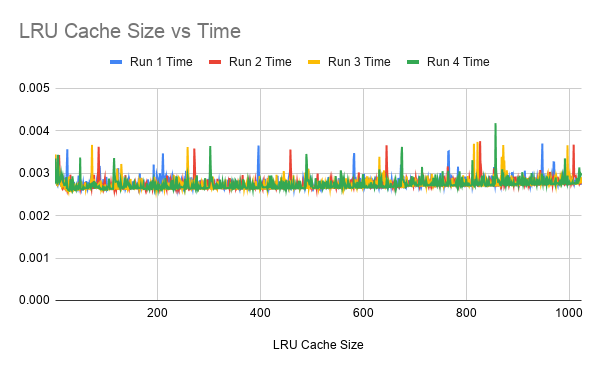
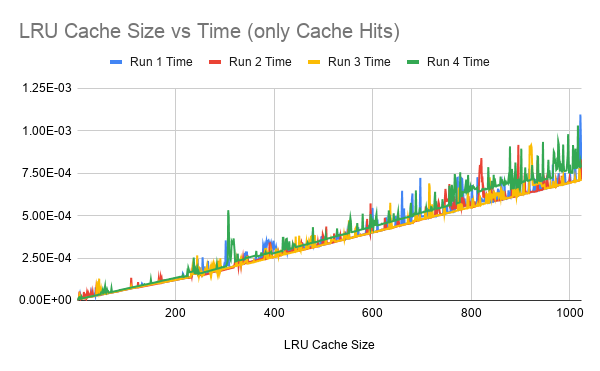
Here's a timing tool demonstrates the impact of different maxsize values:
from time import perf_counter
from functools import lru_cache
from itertools import cycle, islice
def cache_performance(maxsize, times=10**8):
"Performance of *times* misses for a given *maxsize*."
func = lru_cache(maxsize)(type)
data = (object() for i in range(n+1)) # n+1 distinct objects
iterator = islice(cycle(data), times)
start = perf_counter()
for x in iterator:
func(x)
return perf_counter() - start, func.cache_info()
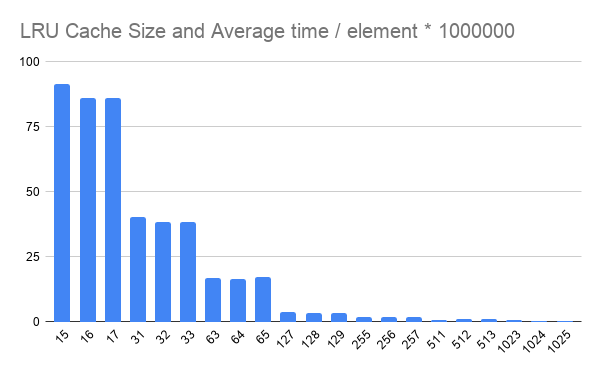
Running it values near the transition optimum shows a small 6% degradation just below the optimum maxsize. This is so small that we don't notice anymore. But when the dict's internal growth rate was only 2x, the degradation was large and devastating:
>>> for n in [699_050, 699_051, 699_052, 699_053]:
... print(*cache_performance(n), sep='\t')
...
15.266257792012766 CacheInfo(hits=0, misses=100000000, maxsize=699050, currsize=699050)
15.06655020796461 CacheInfo(hits=0, misses=100000000, maxsize=699051, currsize=699051)
14.196706458984409 CacheInfo(hits=0, misses=100000000, maxsize=699052, currsize=699052)
14.19534025003668 CacheInfo(hits=0, misses=100000000, maxsize=699053, currsize=699053)
The lru_cache() code exercises its underlying dictionary in an atypical way. While maintaining total constant size, cache misses delete the oldest item and insert a new item.
The size suggestion is an artifact of how this delete-and-insert pattern interacts with the underlying dictionary implementation.
A dict with 2**n * 2 // 3 + 1 entries has the most available space for dummy entries, so the O(n) resizes occur less often.
Also, sparse dictionaries have fewer hash collisions than mostly full dictionaries. Collisions degrade dictionary performance.
The lru_cache() only updates the dictionary when there is a cache miss. Also, when there is a miss, the wrapped function is called. So, the effect of resizes would only matter if there are high proportion of misses and if the wrapped function is very cheap.
Far more important than setting the maxsize just above a resize transition point is using the largest reasonable maxsize. Bigger caches have more cache hits — that's where the big wins come from.
Once an lru_cache() is full and the first resize has occurred, the dictionary settles into a steady state and will never get larger. Here, we simulate what happens next as new dummy entries are added and periodic resizes clear them away.
table_size = 2 ** 7
resize_point = table_size * 2 // 3
def simulate_lru_cache(lru_maxsize, misses=1_000_000):
'Track resize workload as cache misses occur.'
filled = lru_maxsize
resizes = 0
work = 0
for i in range(misses):
filled += 1
if filled >= resize_point:
resizes += 1
work += lru_maxsize # copy active entries
filled = lru_maxsize # dummies not copied
work_per_miss = work / misses
print(lru_maxsize, '→', resizes, work_per_miss)
Here is an excerpt of the output:
>>> for maxsize in range(43, 85):
... simulate_lru_cache(maxsize, sep='\t')
...
43 → 23809 1.023787
44 → 24390 1.07316
45 → 25000 1.125
46 → 25641 1.179486
47 → 26315 1.236805
48 → 27027 1.297296
49 → 27777 1.361073
50 → 28571 1.42855
51 → 29411 1.499961
52 → 30303 1.575756
53 → 31250 1.65625
54 → 32258 1.741932
55 → 33333 1.833315
56 → 34482 1.930992
57 → 35714 2.035698
58 → 37037 2.148146
59 → 38461 2.269199
60 → 40000 2.4
61 → 41666 2.541626
62 → 43478 2.695636
63 → 45454 2.863602
64 → 47619 3.047616
65 → 50000 3.25
66 → 52631 3.473646
67 → 55555 3.722185
68 → 58823 3.999964
69 → 62500 4.3125
70 → 66666 4.66662
71 → 71428 5.071388
72 → 76923 5.538456
73 → 83333 6.083309
74 → 90909 6.727266
75 → 100000 7.5
76 → 111111 8.444436
77 → 125000 9.625
78 → 142857 11.142846
79 → 166666 13.166614
80 → 200000 16.0
81 → 250000 20.25
82 → 333333 27.333306
83 → 500000 41.5
84 → 1000000 84.0
What this shows is that the cache does significantly less work when maxsize is as far away as possible from the resize_point.
The dictionary size transition points are directly observable:
from sys import getsizeof
d = {}
seen = set()
for i in range(1_000_000):
s = getsizeof(d)
d[i] = None
if s not in seen:
seen.add(s)
print(len(d))
On Python 3.13, this reveals the following transition points:
1
2
7
12
23
44
87
172
343
684
1367
2732
5463
10924
21847
43692
87383
174764
349527
699052
The effect was minimal in Python3.2, when dictionaries grew by 4 x active_entries when resizing.
The effect became catastrophic when the growth rate was lowered to 2 x active entries.
Later a compromise was reached, setting the growth rate to 3 x used. That significantly mitigated the issue by giving us a larger steady state size by default.
A power-of-two maxsize is still the optimum setting, giving the least work for a given steady state dictionary size, but it no longer matters as much as it did in Python3.2.
Hope this helps clear up your understanding. :-)
2 x active_entries, plus one, and rounded-up to the new power of two, the jump to the next bigger table size occurred right at a power-of-two. That bigger table gives you the most room for adding dummy entries before the next resize. –
Cleveland TL;DR - this is an optimization that doesn't have much effect at small lru_cache sizes, but (see Raymond's reply) has a larger effect as your lru_cache size gets bigger.
So this piqued my interest and I decided to see if this was actually true.
First I went and read the source for the LRU cache. The implementation for cpython is here: https://github.com/python/cpython/blob/master/Lib/functools.py#L723 and I didn't see anything that jumped out to me as something that would operate better based on powers of two.
So, I wrote a short python program to make LRU caches of various sizes and then exercise those caches several times. Here's the code:
from functools import lru_cache
from collections import defaultdict
from statistics import mean
import time
def run_test(i):
# We create a new decorated perform_calc
@lru_cache(maxsize=i)
def perform_calc(input):
return input * 3.1415
# let's run the test 5 times (so that we exercise the caching)
for j in range(5):
# Calculate the value for a range larger than our largest cache
for k in range(2000):
perform_calc(k)
for t in range(10):
print (t)
values = defaultdict(list)
for i in range(1,1025):
start = time.perf_counter()
run_test(i)
t = time.perf_counter() - start
values[i].append(t)
for k,v in values.items():
print(f"{k}\t{mean(v)}")
I ran this on a macbook pro under light load with python 3.7.7.
Here's the results:
The random spikes are probably due to GC pauses or system interrupts.
At this point I realized that my code always generated cache misses, and never cache hits. What happens if we run the same thing, but always hit the cache?
I replaced the inner loop with:
# let's run the test 5 times (so that we exercise the caching)
for j in range(5):
# Only ever create cache hits
for k in range(i):
perform_calc(k)
The data for this is in the same spreadsheet as above, second tab.
Let's see:
Hmm, but we don't really care about most of these numbers. Also, we're not doing the same amount of work for each test, so the timing doesn't seem useful.
What if we run it for just 2^n 2^n + 1, and 2^n - 1. Since this speeds things up, we'll average it out over 100 tests, instead of just 10.
We'll also generate a large random list to run on, since that way we'll expect to have some cache hits and cache misses.
from functools import lru_cache
from collections import defaultdict
from statistics import mean
import time
import random
rands = list(range(128)) + list(range(128)) + list(range(128)) + list(range(128)) + list(range(128)) + list(range(128)) + list(range(128)) + list(range(128))
random.shuffle(rands)
def run_test(i):
# We create a new decorated perform_calc
@lru_cache(maxsize=i)
def perform_calc(input):
return input * 3.1415
# let's run the test 5 times (so that we exercise the caching)
for j in range(5):
for k in rands:
perform_calc(k)
for t in range(100):
print (t)
values = defaultdict(list)
# Interesting numbers, and how many random elements to generate
for i in [15, 16, 17, 31, 32, 33, 63, 64, 65, 127, 128, 129, 255, 256, 257, 511, 512, 513, 1023, 1024, 1025]:
start = time.perf_counter()
run_test(i)
t = time.perf_counter() - start
values[i].append(t)
for k,v in values.items():
print(f"{k}\t{mean(v)}")
Data for this is in the third tab of the spreadsheet above.
Here's a graph of the average time per element / lru cache size:
Time, of course, decreases as our cache size gets larger since we don't spend as much time performing calculations. The interesting thing is that there does seem to be a dip from 15 to 16, 17 and 31 to 32, 33. Let's zoom in on the higher numbers:
Not only do we lose that pattern in the higher numbers, but we actually see that performance decreases for some of the powers of two (511 to 512, 513).
Edit: The note about power-of-two was added in 2012, but the algorithm for functools.lru_cache looks the same at that commit, so unfortunately that disproves my theory that the algorithm has changed and the docs are out of date.
Edit: Removed my hypotheses. The original author replied above - the problem with my code is that I was working with "small" caches - meaning that the O(n) resize on the dicts was not very expensive. It would be cool to experiment with very large lru_caches and lots of cache misses to see if we can get the effect to appear.
© 2022 - 2024 — McMap. All rights reserved.