Partial Correlation in Python

Question

I ran a correlation matrix:

sns.pairplot(data.dropna())
corr = data.dropna().corr()
corr.style.background_gradient(cmap='coolwarm').set_precision(2)

and it looks like advisory_pct is fairly (0.57) negatively correlated to all_brokerage_pct. As far as I understand, I can claim that we are fairly certain that "when advisor has low % of advisory in his portfolio, he has high % of all brokerage in his portfolio".

However this is a "pairwise" correlation, and we are not controlling for the effect of the rest of the possible variables.

I searched SO and was not able to find how I can run a "partial correlation" where the correlation matrix can provide the correlation between every two variables- while controlling for the rest of the variables. For this purpose lets assume, brokerage % + etf brokerage % + advisory % + all brokerage % = ~100% of portfolio.

Does such function exist?

-- EDIT -- Running the data as per https://stats.stackexchange.com/questions/288273/partial-correlation-in-panda-dataframe-python:

dict = {'x1': [1, 2, 3, 4, 5], 'x2': [2, 2, 3, 4, 2], 'x3': [10, 9, 5, 4, 9], 'y' : [5.077, 32.330, 65.140, 47.270, 80.570]} 
data = pd.DataFrame(dict, columns=['x1', 'x2', 'x3', 'y'])

partial_corr_array = df.as_matrix()
data_int = np.hstack((np.ones((partial_corr_array.shape[0],1)), partial_corr_array))
print(data_int)
[[  1.      1.      2.     10.      5.077]
 [  1.      2.      2.      9.     32.33 ]
 [  1.      3.      3.      5.     65.14 ]
 [  1.      4.      4.      4.     47.27 ]
 [  1.      5.      2.      9.     80.57 ]]
arr = np.round(partial_corr(partial_corr_array)[1:, 1:], decimals=2)
print(arr)
[[ 1.    0.99  0.99  1.  ]
 [ 0.99  1.   -1.   -0.99]
 [ 0.99 -1.    1.   -0.99]
 [ 1.   -0.99 -0.99  1.  ]]
corr_df = pd.DataFrame(arr, columns = data.columns, index = data.columns)
print(corr_df)
    x1    x2    x3    y
x1  1.00  0.99  0.99  1.00
x2  0.99  1.00 -1.00 -0.99
x3  0.99 -1.00  1.00 -0.99
y   1.00 -0.99 -0.99  1.00

These correlations don't make much sense. Using my real data, I get a very similar result where all correlations are rounded to -1..

Hoye

"fairly (0.57) negatively correlated"? That is not a very good correlation at all – Marylouisemaryly

id have a hard time believe anything above .7 (unless it is something that makes sense like age and years of experience) so I think it is fairly correlated. Not really the point though :) – Hoye

You are asking questions about statistics. You are making comments about the statistical quality of the data, and asking what you can dedude from it. That is not a question suitable for SO in that aspect. You should probably be asking about that part in Stats or Mathematics – Marylouisemaryly

And to be honest, I think that 1) either your data samples are not good, 2) you are not analizing the data correctly, or 3) the data does not have any specific correlation that can be known; the graphs you show have very very bad correlation trends (but that should be said probably by an expert from those sites mentioned) – Marylouisemaryly

From what I know about stats, good correlation is above 0.75, and when talking about scientific experimental results it usually has to be around 0.85-0.9. – Marylouisemaryly

@J.C.Rocamonde I am not disagreeing but that isnt really the point of the question. I am asking for a partial correlation function, and then whatever the result is- I can evaluate the correlation significance from there – Hoye

Yeah, well; not trying to dishearten your question, but to be honest I think that is exactly what you are asking: "can I for example say that "if advisor has <10% in advisory, we are fairly certain he has >90% in all brokerage"?" that is a stats question for me. Not programming. – Marylouisemaryly

trying to help you here, honestly its better if you first get to know the mathematical concepts you have to use exactly, and how to analyse your data, and then once you know that you can ask for the specific implementation in code of what you want to use. But you kind of still seem indecise about that part, so you will find little help with it here. That is my advice, with all best hope. – Marylouisemaryly

You may want to take a look at this SO question: #44843634 – Marylouisemaryly

And this stats.stackexchange.com/questions/288273/… – Marylouisemaryly

Dropped stats question, only left function request. First link seems to only rank the pairwise correlations. Second one is exactly what I did but gives a more readable output. I think that can work actually – Hoye

I'm not telling you to not ask; just that it's better if you ask that in a stats site. I encourage you to ask any stats question you have ;) as for the function request, have you looked in scipy docs? Did you find something? Maybe thats a good starting point for the question – Marylouisemaryly

yeah went through scipy – Hoye

By looking at the -0.57 chart the area is just limited by functionsl bound and dots dispersed sparringly within. Your number is reflection there is a functional bound, but link between variables is poor. – Brack

I think it is pretty hard to say whether the ones or negative ones are reasonable, when regression is done on all other variables - try using random.randint instead, which promises no unwanted correlation between variables. – Kyles

@Kyles Thank you for this. Ill need some time to go through your edit. Will try to use edit 1 data on your function from edit 2 as well. Can you just explain the reasoning behind the +- np.random.randint() your chose for the various variables? – Hoye

So that there are no unwanted correlations between variables other than the ones we intentionally set. – Kyles

@Kyles As per your most recent edit- I understand how this will work for the random data you created, but how would you use the randomization concept you create to actual data? example: dict = {'x1': [1, 2, 3, 4, 5], 'x2': [2, 2, 3, 4, 2], 'x3': [10, 9, 5, 4, 9], 'y' : [5.077, 32.330, 65.140, 47.270, 80.570]} data = pd.DataFrame(dict, columns=['x1', 'x2', 'x3', 'y']) – Hoye

Answer 1

AFAIK, there is no official implementation of partial correlation in scipy / numpy. As pointed out by @J. C. Rocamonde, the function from that stats website can be used to calculate partial correlation.

I believe here's the original source:

https://gist.github.com/fabianp/9396204419c7b638d38f

Note:

1. As discussed in the github page, you may want to add a column of ones to add a bias term to your fits if your data is not standardized (Judging from your data it's not).

2. If I'm not mistaken, it calculates partial correlation by controlling all other remaining variables in the matrix. If you just want to control one variable, you may change idx to the index of that particular variable.

---

Edit 1 (How to add ones + What to do with df):

If you look into the link, they have already discussed how to add ones.

To illustrate how it works, I added another way of hstack, using the given data in the link:

data_int = np.hstack((np.ones((data.shape[0],1)), data)) 
test1 = partial_corr(data_int)[1:, 1:]
print(test1)

# You can also add it on the right, as long as you select the correct coefficients
data_int_2 = np.hstack((data, np.ones((data.shape[0],1)))) 
test2 = partial_corr(data_int_2)[:-1, :-1]
print(test2)

data_std = data.copy() 
data_std -= data.mean(axis=0)[np.newaxis, :] 
data_std /= data.std(axis=0)[np.newaxis, :] 
test3 = partial_corr(data_std)
print(test3)

Output:

[[ 1.         -0.54341003 -0.14076948]
 [-0.54341003  1.         -0.76207595]
 [-0.14076948 -0.76207595  1.        ]]
[[ 1.         -0.54341003 -0.14076948]
 [-0.54341003  1.         -0.76207595]
 [-0.14076948 -0.76207595  1.        ]]
[[ 1.         -0.54341003 -0.14076948]
 [-0.54341003  1.         -0.76207595]
 [-0.14076948 -0.76207595  1.        ]]

And if you want to maintain the columns, easiest way is to extract the columns and put them back in after calculation:

# Assume that we have a DataFrame with columns x, y, z
data_as_df = pd.DataFrame(data, columns=['x','y','z'])
data_as_array = data_as_df.values
partial_corr_array = partial_corr(np.hstack((np.ones((data_as_array.shape[0],1)), data_as_array))
                                 )[1:,1:]
corr_df = pd.DataFrame(partial_corr_array, columns = data_as_df.columns)
print(corr_df)

Output:

       x      y      z
0  1.000 -0.543 -0.141
1 -0.543  1.000 -0.762
2 -0.141 -0.762  1.000

Hope it's helpful! Let me know if anything is unclear!

---

Edit 2:

I think the problem lies in not having constant term in each of the fits... I rewrote the code in sklearn to make it easier to add intercept:

def calculate_partial_correlation(input_df):
    """
    Returns the sample linear partial correlation coefficients between pairs of variables,
    controlling for all other remaining variables

    Parameters
    ----------
    input_df : array-like, shape (n, p)
        Array with the different variables. Each column is taken as a variable.

    Returns
    -------
    P : array-like, shape (p, p)
        P[i, j] contains the partial correlation of input_df[:, i] and input_df[:, j]
        controlling for all other remaining variables.
    """
    partial_corr_matrix = np.zeros((input_df.shape[1], input_df.shape[1]));
    for i, column1 in enumerate(input_df):
        for j, column2 in enumerate(input_df):
            control_variables = np.delete(np.arange(input_df.shape[1]), [i, j]);
            if i==j:
                partial_corr_matrix[i, j] = 1;
                continue
            data_control_variable = input_df.iloc[:, control_variables]
            data_column1 = input_df[column1].values
            data_column2 = input_df[column2].values
            fit1 = linear_model.LinearRegression(fit_intercept=True)
            fit2 = linear_model.LinearRegression(fit_intercept=True)
            fit1.fit(data_control_variable, data_column1)
            fit2.fit(data_control_variable, data_column2)
            residual1 = data_column1 - (np.dot(data_control_variable, fit1.coef_) + fit1.intercept_)
            residual2 = data_column2 - (np.dot(data_control_variable, fit2.coef_) + fit2.intercept_)
            partial_corr_matrix[i,j] = stats.pearsonr(residual1, residual2)[0]
    return pd.DataFrame(partial_corr_matrix, columns = input_df.columns, index = input_df.columns)

# Generating data in our minion world
test_sample = 10000;
Math_score = np.random.randint(100,600, size=test_sample) + 20 * np.random.random(size=test_sample)
Eng_score = np.random.randint(100,600, size=test_sample) - 10 * Math_score + 20 * np.random.random(size=test_sample)
Phys_score = Math_score * 5 - Eng_score + np.random.randint(100,600, size=test_sample) + 20 * np.random.random(size=test_sample)
Econ_score = np.random.randint(100,200, size=test_sample) + 20 * np.random.random(size=test_sample)
Hist_score = Econ_score + 100 * np.random.random(size=test_sample)

minions_df = pd.DataFrame(np.vstack((Math_score, Eng_score, Phys_score, Econ_score, Hist_score)).T, 
                          columns=['Math', 'Eng', 'Phys', 'Econ', 'Hist'])

calculate_partial_correlation(minions_df)

Output:

----  ----------  -----------  ------------  -----------  ------------
Math   1          -0.322462     0.436887     0.0104036    -0.0140536
Eng   -0.322462    1           -0.708277     0.00802087   -0.010939
Phys   0.436887   -0.708277     1            0.000340397  -0.000250916
Econ   0.0104036   0.00802087   0.000340397  1             0.721472
Hist  -0.0140536  -0.010939    -0.000250916  0.721472      1
----  ----------  -----------  ------------  -----------  ------------

Please let me know if that's not working!

Kyles

Is the position of 1s important? – Hoye

Also, how would you recommend adding the 1s while keeping it as a dataframe, and not numpy array? – Hoye

I am actually using the data as per stats.stackexchange.com/questions/288273/… and running into an issue- see edited question – Hoye

Do you want to control over all other variables or over specific variables? – Kyles

I believe it should be all. In my data we are looking at portfolio allocation, where all variables add up to 100% – Hoye

I'll try to look into that more deeply during the weekend – Kyles

Answer 2

To compute the correlation between two columns of a pandas DataFrame whilst controlling for one or more covariates (i.e. other columns in the dataframe), you can use the partial_corr function of the Pingouin package (disclaimer, of which I am the creator):

from pingouin import partial_corr
partial_corr(data=df, x='X', y='Y', covar=['covar1', 'covar2'], method='pearson')

Lyontine

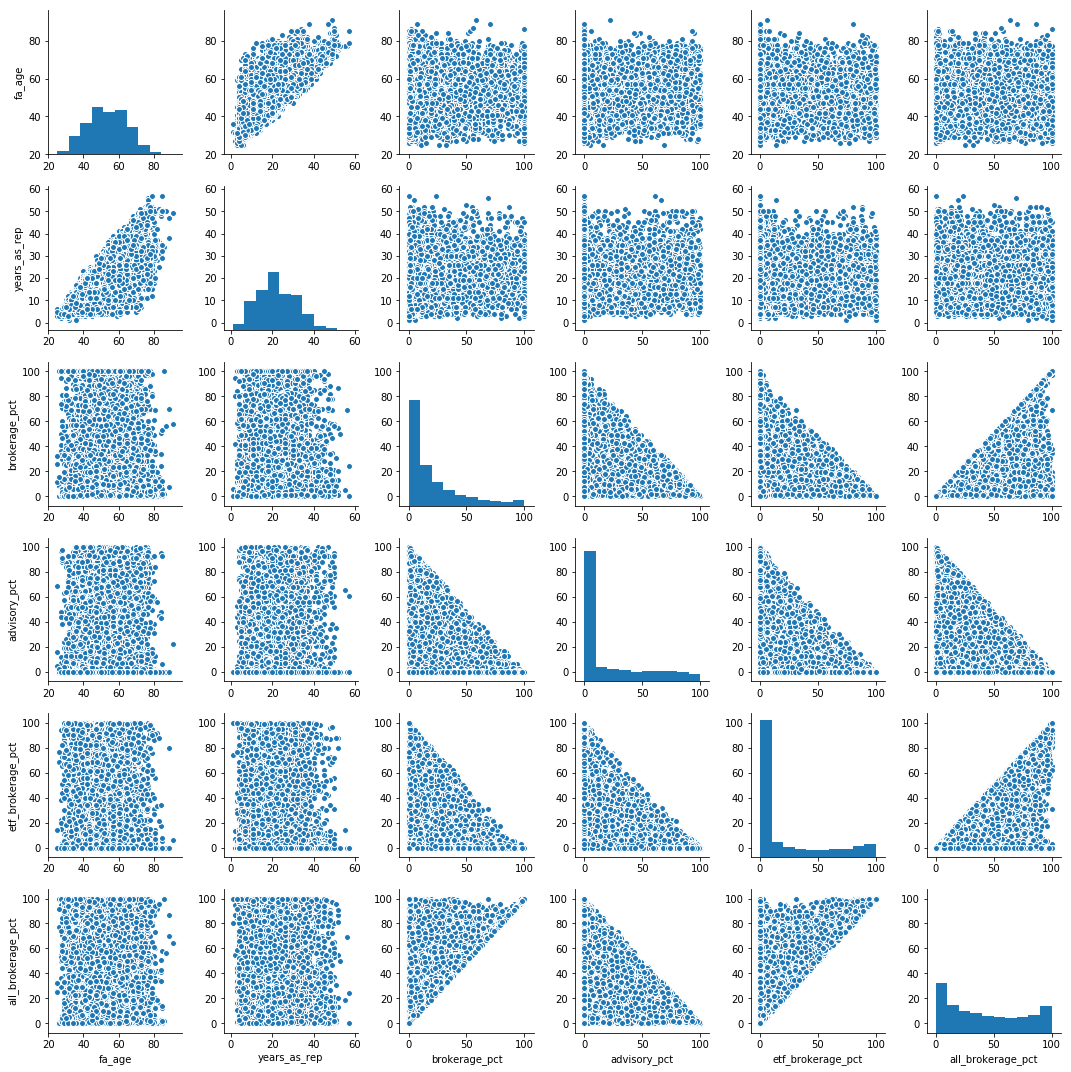
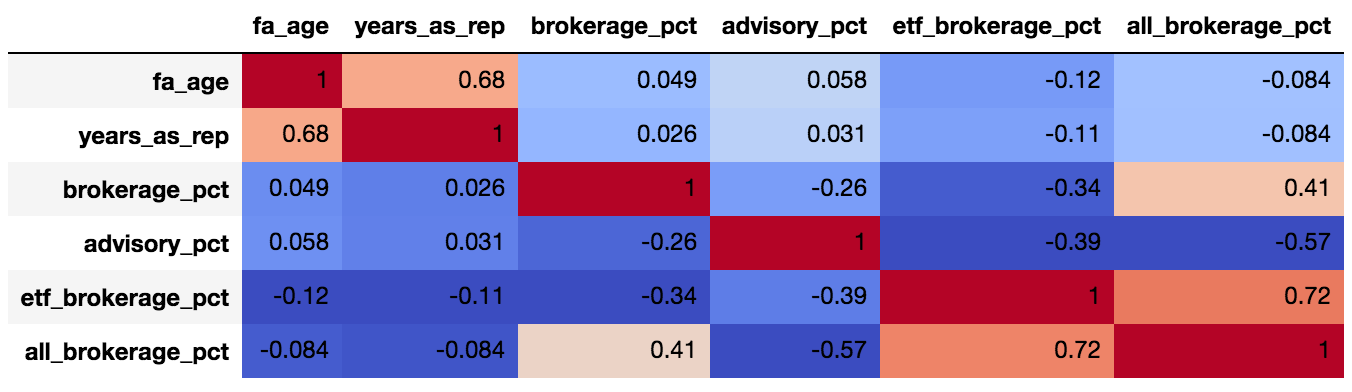
Very impressive, thank you! Can you run this for: dict = {'x1': [1, 2, 3, 4, 5], 'x2': [2, 2, 3, 4, 2], 'x3': [10, 9, 5, 4, 9], 'y' : [5.077, 32.330, 65.140, 47.270, 80.570]} data = pd.DataFrame(dict, columns=['x1', 'x2', 'x3', 'y']) and let me know if your result differs from result in -- EDIT -- section of the question? – Hoye

No the results do not differ however the partial_corr function only returns one correlation coefficient between a priori specified variables and not a correlation matrix between all columns of a dataframe. So for instance, using your example data, the following lines: partial_corr(data=data, x='x1', y='y', covar=['x2', 'x3']) gives a DataFrame (r = 0.998,95%CI = [0.97, 1.0], r^2 = 0.996, p-val=0.000102, Bayes Factor = 225) – Lyontine

Is it possible to somehow apply this as a correlation matrix between all columns of a dataframe? – Hoye

Yes, since v0.2.4 it is now possible to compute a partial correlation between all the pairwise columns of a dataframe using the pairwise_corr function (see pingouin-stats.org/generated/pingouin.pairwise_corr.html) – Lyontine

Or, if you prefer to keep the matrix format, see also the pingouin.pcorr method. – Lyontine

Answer 3

Half-line code:

import numpy as np

X=np.random.normal(0,1,(5,5000)) # 5 variable stored as rows
Par_corr = -np.linalg.inv(np.corrcoef(X)) # 5x5 matrix

Sobriety

Answer 4

The matrix of partial correlations is a scaled inverse of the covariance matrix.

def partial_correlation(X: pd.DataFrame):
    X = X.select_dtypes(['number'])
    precision = np.linalg.inv(X.cov())
    diag = np.diag(precision)
    Z = np.outer(diag, diag)
    partial = -precision / Z
    return pd.DataFrame(partial, columns=X.columns, index=X.columns)

If you also want to test for significance, I would recommend running bootstrap simulation as this is most intuitive and easy to implement.

Source: Ryan Tibshirani Lecture Spring 2017: Statistical Machine Learning (10-702/36-702) -- Lecture 22: Graphical models https://www.youtube.com/watch?v=Cdpfpy4bXPI&list=PLjbUi5mgii6B7A0nM74zHTOVQtTC9DaCv&index=23

PS: Depending on your problem the empirical covariance without any regularization may not be the best choice, so if you have many dimensions or noisy observations you may want to check the more robust covariance estimators from scikit-learn https://scikit-learn.org/stable/modules/covariance.html#covariance

Specify

How do you specify the reference variable here? – Dallas

In the partial correlation between X and Y given Z, do you refer to Z as the reference variable? In that case, Z is all the other variables in your dataframe. Let's say you have a set of variables {A, B, C, D}, then the partial correlation matrix contains all combinations. For example the correlation of A with C given B and D. – Specify

Interesting! Is that similar to this implementation? github.com/tpq/propr/blob/… – Dallas

Answer 5

You can try this:

from sklearn.linear_model import LinearRegression
from scipy.stats import pearsonr

feature_num = df.shape[1]
feature_name = df.columns
partial_corr_matrix = np.zeros((feature_num, feature_num))
for i in range(feature_num):
    x1 = df.iloc[:, i]
    for j in range(feature_num):
        if i == j:
            partial_corr_matrix[i, j] = 1
        elif j < i:
            partial_corr_matrix[i, j] = partial_corr_matrix[j, i]
        else:
            x2 = df.iloc[:, j]
            df_control = df.drop(columns=[feature_name[i], feature_name[j]], axis=1)
            L = LinearRegression().fit(df_control, x1)
            Lx = L.predict(df_control)
            x1_prime = x1 - Lx
            
            L = LinearRegression().fit(df_control, x2)
            Lx = L.predict(df_control)
            x2_prime = x2 - Lx
            partial_corr_matrix[i, j] = pearsonr(x1_prime, x2_prime)[0]

Ferroelectric

there's already quite a few answers. Can you add some explanation to your code and how it is different from the others? – Colligan