Applying Fourier Transform on Time Series data and avoiding aliasing

Question

I am willing to apply Fourier transform on a time series data to convert data into frequency domain. I am not sure if the method I've used to apply Fourier Transform is correct or not? Following is the link to data that I've used.

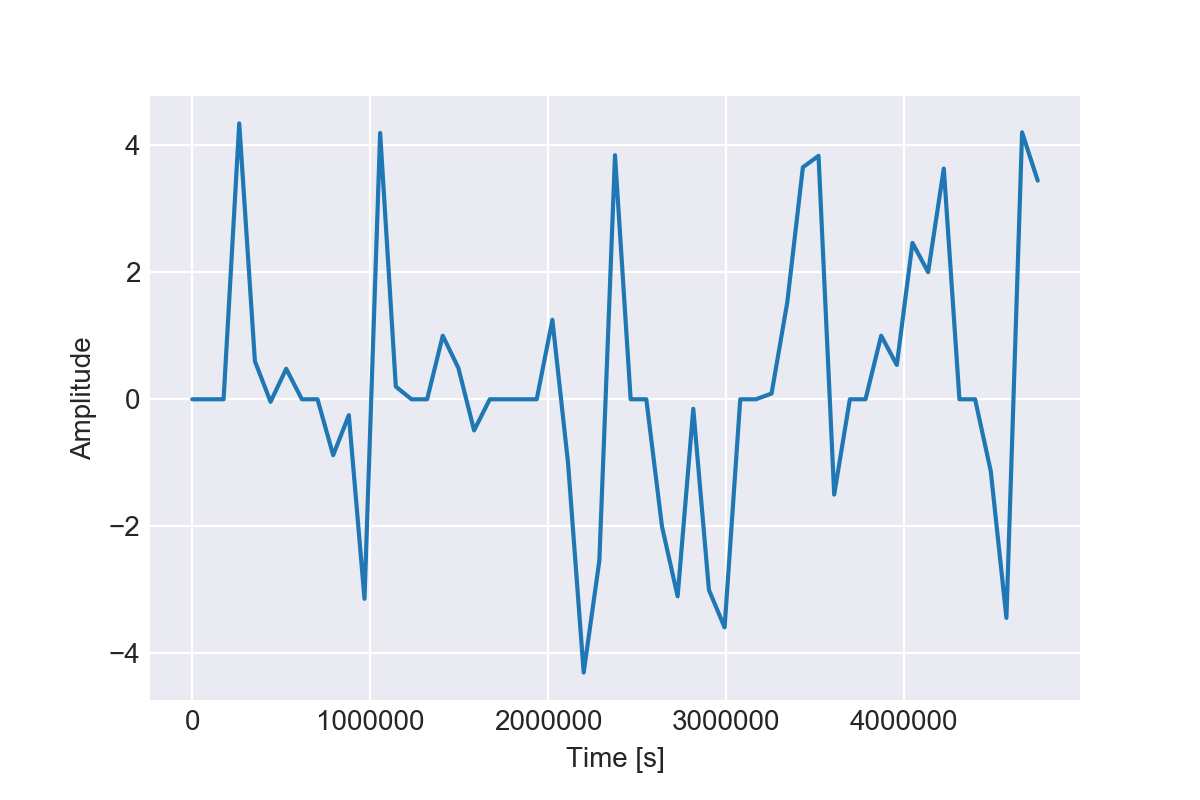
After reading the data file I've plotted original data using

t = np.linspace(0,55*24*60*60, 55)
s = df.values
sns.set_style("darkgrid")
plt.ylabel("Amplitude")
plt.xlabel("Time [s]")
plt.plot(t, s)
plt.show()

Since the data is on a daily frequency I've converted it into seconds using 24*60*60 and for a period of 55 days using 55*24*60*60

The graph looks as follows:

Next I've implemeted Fourier Transform using following piece of code and obtained the image as follows:

#Applying Fourier Transform
fft = fftpack.fft(s)

#Time taken by one complete cycle of wave (seconds)
T = t[1] - t[0] 

#Calculating sampling frequency
F = 1/T

N = s.size

#Avoid aliasing by multiplying sampling frequency by 1/2 
f = np.linspace(0, 0.5*F, N)

#Convert frequency to mHz
f = f * 1000

#Plotting frequency domain against amplitude
sns.set_style("darkgrid")
plt.ylabel("Amplitude")
plt.xlabel("Frequency [mHz]")
plt.plot(f[:N // 2], np.abs(fft)[:N // 2])  
plt.show()

I've following questions:

I am not sure if my above methodology is correct to implement Fourier Transform.

I am not sure if the method I am using to avoid aliasing is correct.

If, what I've done is correct than how to interpret the three peaks in Frequency domain plot.

Finally, how would I invert transform using only frequencies that are significant.

Utta

Just for the record, in case people come here copy-pasting code: f = np.linspace(0, 0.5*F, N) is wrong. I suggest you use np.fft.fftfreq() to compute the frequency values associated to each sample. – Cue

Answer 1

While I'd refrain from answering your first two questions (it looks okay to me but I'd love an expert's input), I can weigh in on the latter two:

If, what I've done is correct than how to interpret the three peaks in Frequency domain plot.

Well, that means you've got three main components to your signal at frequencies roughly 0.00025 mHz (not the best choice of units here, possibly!), 0.00125 mHz and 0.00275 mHz.

Finally, how would I invert transform using only frequencies that are significant.

You could just zero out every frequency below a cutoff you decide (say, absolute value of 3 - that should cover your peaks here). Then you can do:

below_cutoff = np.abs(fft) < 3
fft[below_cutoff] = 0
cleaner_signal = fftpack.ifft(fft)

And that should do it, really!

Pleasant

Answer 2

The code seems to be okay, and no, you don't have aliasing, because of that 0.5*F.

Aliasing is related not to the signal itself, but rather to how you acquire the signal.

According to Nyquist theorem you have:

for a given sample rate f_s, perfect reconstruction is guaranteed possible for a bandlimit B < f_s/2.

In other words it's the sampling frequency that determines aliasing.

Example:

If you have a signal that has two frequency components at 5 kHz and 8 kHz, and you acquire the signal with f_s = 12 kHz, you'll see clearly all frequency components up to 6 kHz (f_s/2), while for greater frequencies you'll have aliasing, i.e. the information is distorted.

In this example you'd see clearly the 5 kHz component, but not the 8 kHz one, because it's beyond f_s/2 (this value is also called Nyquist frequency).

What your code is telling is: with the sampling frequency F, i can show clearly all signal components up to F/2, and in fact in below chart, you correctly plot the fft up to F/2; greater frequencies are disorted because of aliasing.

Remember: aliasing is due to a sampling frequency too low for the frequency components that you want to investigate

Grison

"greater frequencies are distorted because of aliasing" This makes no sense. Frequencies at Nyquist and above that existed in the signal before sampling get aliased to lower frequencies. If the signal was not appropriately bandlimited, then it is the lower frequencies that get distorted due to aliasing, the higher frequencies do not exist in the sampled signal. -- But the FFT computes the Discrete Fourier Transform, which is not the same as the (continuous-domain) Fourier Transform. The DFT has frequencies 0 to N-1, with the second half being complex-conjugate symmetric of the first half. – Cue